
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
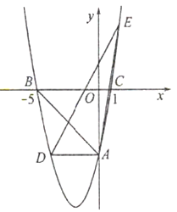
(1)求此抛物线的表达式;
(2)点![]() 是抛物线上一点,且点
是抛物线上一点,且点![]() 关于
关于![]() 轴的对称点在直线
轴的对称点在直线![]() 上,求
上,求![]() 的面积;
的面积;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上一动点,当点
下方的抛物线上一动点,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的面积最大,求出此时点
的面积最大,求出此时点![]() 的坐标和
的坐标和![]() 的最大面积.
的最大面积.
【答案】(1)y=x2+4x-5;(2)20;(3)点P的坐标是(![]() ,-
,-![]() )时,△ABP的面积最大,此时△ABP的面积是
)时,△ABP的面积最大,此时△ABP的面积是![]() .
.
【解析】(1)用待定系数法求出二次函数的解析式即可.
(2)根据点E的纵坐标是5,求出点E到AD的距离是10,求出点D的坐标,计算出![]() 的长度,即可求出
的长度,即可求出![]() 的面积;
的面积;
(3)设点P的坐标为(p,p2+4p-5),用待定系数法求出直线AB的解析式,列出关于△ABP的面积的式子,根据二次函数的性质即可求出面积的最大值.
(1)∵抛物线![]() 交y轴于点A,交x轴于点B(-5,0)和点C(1,0),
交y轴于点A,交x轴于点B(-5,0)和点C(1,0),
∴![]() ,得
,得![]() ,
,
∴此抛物线的表达式是y=x2+4x-5;
(2)∵抛物线y=x2+4x-5交y轴于点A,
∴点A的坐标为(0,-5),
∵AD∥x轴,点E是抛物线上一点,且点E关于x轴的对称点在直线AD上,
∴点E的纵坐标是5,点E到AD的距离是10,
当y=-5时,-5=x2+4x-5,得x=0或x=-4,
∴点D的坐标为(-4,-5),
∴AD=4,
∴△EAD的面积是:![]() =20;
=20;
(3)设点P的坐标为(p,p2+4p-5),如图所示,
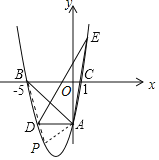
设过点A(0,-5),点B(-5,0)的直线AB的函数解析式为y=mx+n,![]() ,得
,得![]() ,
,
即直线AB的函数解析式为![]()
当![]() 时,
时,![]()
∵OB=5,
∴△ABP的面积是:S=![]() ,
,
∵点![]() 是直线
是直线![]() 下方的抛物线上一动点,
下方的抛物线上一动点,
∴-5<![]() <0,
<0,
∴当![]() =-
=-![]() 时,
时,![]() 取得最大值,此时S=
取得最大值,此时S=![]() ,点p的坐标是(
,点p的坐标是(![]() ,-
,-![]() ),
),
即点p的坐标是(![]() ,-
,-![]() )时,△ABP的面积最大,此时△ABP的面积是
)时,△ABP的面积最大,此时△ABP的面积是![]() .
.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
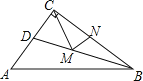
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,某市决定调整居民用水收费方法,规定如果每户每月用水不超过10吨,每吨水收费2元,如果每户每月用水超过10吨,则超过部分每吨水收费2.5元;小红看到这种收费方法后,想算算她家每月的水费:
(1)如果小红家每月用水8吨,则水费是 元;如果小红家每月用水20吨,则水费是 元.
(2)如果字母![]() 表示小红家每月用水的吨数,那么小红家每月的水费该如何用
表示小红家每月用水的吨数,那么小红家每月的水费该如何用![]() 的代数式表示呢?
的代数式表示呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下列材料,再解决后面的问题.
依照平方根(即二次方根)和立方根(即三次方根)的定义,可给出四次方根、五次方根的定义.比如:若x2=a(a≥0),则x叫a的二次方根;若x3=a,则x叫a的三次方根:若x4=a(a≥0),则x叫a的四次方根;
(1)依照上面的材料,请你给出五次方根的定义,并求出﹣32的五次方根;
(2)解方程:![]() (2x﹣4)4﹣8=0
(2x﹣4)4﹣8=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:

请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n= ;
(2)请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;
(3)现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生. 李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
![]()
(1)根据记录的数据可知该厂星期四生产自行车________ 辆;
(2)根据记录的数据可知该厂本周实际生产自行车______辆;
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖励15元;少生产一辆另扣20元,那么该厂工人这一周的工资总额是多少?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com