Question

【题目】如图所示，在等边三角形ABC中，点D是BC边上的一点，且BD＝2CD，P是AD上的一点，∠CPD＝∠ABC，求证：BP⊥AD．

Answer 1

【答案】详见解析

【解析】

作AH⊥BC于H, 因为△ABC为等边三角形，BD＝2CD，即可得CD＝2DH.证明△DPC∽△DCA可得，又因为∠BDP＝∠ADH，可证△DBP∽△DAH，由相似三角形的性质即可得到∠DPB＝∠DHA＝90°，BP⊥AD.

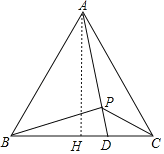
证明：作AH⊥BC于H，如图，

∵△ABC为等边三角形，

∴BH＝CH，∠ABC＝∠ACB＝60°，

∵BD＝2CD，

∴BH＝（BD+CD）＝CD，

∴DH＝BD﹣BH＝2CD﹣CD＝CD，即CD＝2DH，

∵∠CPD＝∠ABC＝∠ACD，

∠PDC＝∠CDA，

∴△DPC∽△DCA，

∴＝DPDA，

∴CD2DH＝DPDA，

∴2CDDH＝DPDA，

∴BDDH＝DPDA，

即，

而∠BDP＝∠ADH，

∴△DBP∽△DAH，

∴∠DPB＝∠DHA＝90°，

∴BP⊥AD．