练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A，B两点，交y轴的正半轴于C点，如果x=a时，y＜0，那么关于x的一次函数y=（a﹣1）x+m的图象可能是（ ）

    A.
    B.
    C.
    D.

    【答案】A
    【解析】解：把x=a代入函数y=x2﹣x+m，得y=a2﹣a+m=a（a﹣1）+m，

    ∵x=a时，y＜0，即 a（a﹣1）+m＜0．

    由图象交y轴的正半轴于点C，得m＞0，

    即a（a﹣1）＜0．

    x=a时，y＜0，∴a＞0，a﹣1＜0，

    ∴一次函数y=（a﹣1）x+m的图象过一二四象限，

    故答案为：A．

    由x=a时，y＜0，把x=a代入二次函数，由图象交y轴的正半轴于点C，得m＞0，求出a＞0，a﹣1＜0，得到一次函数的图象过一二四象限.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、 乙两家超市以相同的价格出售同样的商品．为了吸引顾客，各自推出不同的优惠方案： 在甲超市累计购买商品超出 300 元之后，超出部分按原价八折优惠；在乙超市累计购买商品超出 200 元之后，超出部分按原价九折优惠．设顾客预计累计购物 元( 300)

    （1）请用x 的代数式分别表示顾客在两家超市购物所付的费用；

    （2）试比较顾客到哪家超市购物更优惠？ 说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=mx+n与正比例函数y=mnx（m，n为常数，且mn≠0，n＞0）的图象是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“阳光体育”活动时间，小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛，要从中选出两位同学打第一场比赛．
    （1）若已确定小英打第一场，再从其余三位同学中随机选取一位，求恰好选中小丽同学的概率；
    （2）用画树状图或列表的方法，求恰好选中小敏、小洁两位同学进行比赛的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知反比例函数 的图象经过点（ ，8），直线y=﹣x+b经过该反比例函数图象上的点Q（4，m）．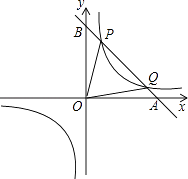

    （1）求上述反比例函数和直线的函数表达式；
    （2）设该直线与x轴、y轴分别相交于A、B两点，与反比例函数图象的另一个交点为P，连接0P、OQ，求△OPQ的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在等边三角形ABC中，点D是BC边上的一点，且BD＝2CD，P是AD上的一点，∠CPD＝∠ABC，求证：BP⊥AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)请在横线上填写合适的内容，完成下面的证明：

    如图①如果AB∥CD，求证：∠APC＝∠A+∠C．

    证明：过P作PM∥AB．

    所以∠A＝∠APM，(　 　)

    因为PM∥AB，AB∥CD(已知)

    所以∠C＝　 　(　 　)

    因为∠APC＝∠APM+∠CPM

    所以∠APC＝∠A+∠C(等量代换)

    (2)如图②，AB∥CD，根据上面的推理方法，直接写出∠A+∠P+∠Q+∠C＝　 　．

    (3)如图③，AB∥CD，若∠ABP＝x，∠BPQ＝y，∠PQC＝z，∠QCD＝m，则m＝　 　(用x、y、z表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为学生开展拓展性课程，拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区（如图1），要求两个大棚之间有间隔4米的路，设计方案如图2，已知每个大棚的周长为44米．

    （1）求每个大棚的长和宽各是多少？

    （2）现有两种大棚造价的方案，方案一是每平方米60元，超过100平方米优惠500元，方案二是每平方米70元，超过100平方米优惠总价的20%，试问选择哪种方案更优惠？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．

    （1）求证：GF=GC；

    （2）用等式表示线段BH与AE的数量关系，并证明．

    查看答案和解析>>

    同步练习册答案