
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 题中没有指明AO,BO,AB是底还是腰,故应该分情况进行分析,注意不但要考虑到AO,BO,AB是底还是腰,而且要考虑A,B是在正半轴还是在负半轴.
解答 解:(1)当AO,BO为腰时,
①当AO=BO(B在Y轴正半轴上),
∵点A坐标为(3,3),O为坐标原点,
∴OA=OB=3$\sqrt{2}$,
∴B1=(0,3$\sqrt{2}$),
②当AO=BO(B在Y轴负半轴上),
同理:B2=(0,-3$\sqrt{2}$).
③当AO=BO(B在X轴正半轴上),
同理:B3=(3$\sqrt{2}$,0).
④当AO=BO(B在X轴负半轴上),
同理:B4=(-$3\sqrt{2}$,0).
(2)当AO为底时,
⑤AB=BO(B在Y轴正半轴上),
同理:B7=(0,3).
⑥当AB=BO(B在X轴正半轴上),
同理:B8=(3,0).
故选B.
点评 此题主要考查等腰三角形的性质及坐标与图形性质的综合运用,注意分类讨论思想的运用.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:选择题
| A. | (5,1) | B. | (-1,1) | C. | (5,5) | D. | (-1,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
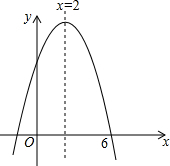 二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=2,若此抛物线与x轴的一个交点为(6,0),则抛物线与x轴的另一个交点坐标是(-2,0).
二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=2,若此抛物线与x轴的一个交点为(6,0),则抛物线与x轴的另一个交点坐标是(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
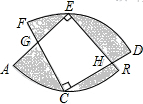 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 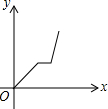 | B. |  | C. | 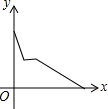 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com