
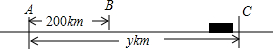 �ú�������ʽ��ʾ���б仯��������������֮��Ĺ�ϵ����ָ�����е�һ�κ�����������������
�ú�������ʽ��ʾ���б仯��������������֮��Ĺ�ϵ����ָ�����е�һ�κ��������������������� ����һ�κ����������������Ķ��壬�ɵô𰸣�
��� �⣺��1��S=a2���ɱ���ʽ��֪�����߳�����������������ϵ��
��2��l=4x���ɱ���ʽ��֪�ܳ���߳���������������ϵ��
��3��S=ax���ɱ���ʽ��֪S��x��������������ϵ��
��4��y=300t���ɱ���ʽ��֪·��y����ʻʱ��t��������������ϵ��
��5��y=200+120t���ɱ���ʽ��֪·��y����ʻʱ��t��һ�κ�����ϵ��
���� ���⿼����һ�κ����������������Ķ��壬����y=kx��k�Dz�����0�ij�������ʽ����������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
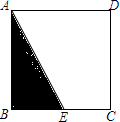 ij�˶�����һ����ͼ��ʾ�ĵ�ש��ÿ���ש���DZ߳�Ϊ��x+3y���������Σ���E��������ABCD�ı�BC�ϣ�EC=��x+y���ף���֪x+3y=5�ף�x+2y=4�ף����ı���AECD�������
ij�˶�����һ����ͼ��ʾ�ĵ�ש��ÿ���ש���DZ߳�Ϊ��x+3y���������Σ���E��������ABCD�ı�BC�ϣ�EC=��x+y���ף���֪x+3y=5�ף�x+2y=4�ף����ı���AECD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
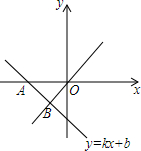 ��ͼ��ֱ��y=kx+b������A��-2��0���͵㣨-1��-1������D��ֱ��y=x�ϣ���ʽx��kx+b�Ľ�Ϊ��������
��ͼ��ֱ��y=kx+b������A��-2��0���͵㣨-1��-1������D��ֱ��y=x�ϣ���ʽx��kx+b�Ľ�Ϊ��������| A�� | x��-1 | B�� | x��-1 | C�� | x��0 | D�� | x��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com