
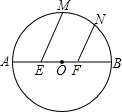
 如图,AB为⊙O的直径,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,则直径AB的长为6.
如图,AB为⊙O的直径,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,则直径AB的长为6. 分析 延长ME交⊙O于G,过点O作OH⊥MG于H,连接MO,过O作OP⊥FN,垂足为P,首先证明FN=EG,根据圆的直径求出OE,OM,再解直角三角形求出OH,然后利用勾股定理列式求出MH,再根据垂径定理可得MG=2MH,从而得解.
解答 解:延长ME交⊙O于G,过点O作OH⊥MG于H,连接MO,过O作OP⊥FN,垂足为P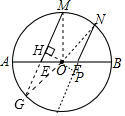
因为O为AB的中点,E,F为AB的三等分点,所以OE=OF,
又因为MG∥FN,
∴∠MEF=∠NFB=∠OFP
∵∠OHG=∠OPF=90°
∴△OHE≌△OPF
∴OH=OP,
同理可证Rt△OHG≌Rt△OPN,
∴∠G=∠N
易证△OEG≌△OFN,
∴EG=FN,
∵⊙O的直径AB=x,
∴OE=OA-AE=$\frac{1}{2}$x-$\frac{1}{3}$x=$\frac{1}{6}$x,
OM=$\frac{1}{2}$x,
∵∠MEB=60°,
∴OH=OE•sin60°=$\frac{x}{6}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}x}{12}$,
在Rt△MOH中,MH=$\sqrt{O{M}^{2}-O{H}^{2}}$=$\sqrt{(\frac{x}{2})^{2}-(\frac{\sqrt{3}x}{12})^{2}}$=$\sqrt{\frac{36{x}^{2}-3{x}^{2}}{144}}$=$\frac{\sqrt{33{x}^{2}}}{12}$,
根据垂径定理,MG=2MH=2×$\frac{\sqrt{33{x}^{2}}}{12}$=$\frac{\sqrt{33}x}{6}$,
即EM+FN=$\frac{\sqrt{33}x}{6}$=$\sqrt{33}$.
解得x=6,
故答案为:6.
点评 本题考查了垂径定理,勾股定理的应用,以及解直角三角形,作辅助线并根据圆的中心对称性得到FN=EG是解题的关键,也是本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码 | 170 | 175 | 180 | 185 | 190 |
| 平均每天的销售量/件 | 7 | 9 | 18 | 10 | 6 |
| A. | 20件 | B. | 18件 | C. | 36件 | D. | 50件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把下面的语句还原成图形:
把下面的语句还原成图形:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )| A. | a>b>c | B. | a=b=c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com