
分析 根据三次项系数为1可设另一个因式为(x+k),将原式变形为x3+mx2+nx+p=(x-1)(x+4)(x+k)=x3+(k+3)x2+(3k-4)x-4k,可得$\left\{\begin{array}{l}{m=k+3}\\{n=3k-4}\\{p=-4k}\end{array}\right.$,代入2m-2n-p+86可得答案.
解答 解:∵x-1,x+4均为多项式x3+mx2+nx+p的因式,且三次项系数为1,
∴设另一个因式为(x+k),
则x3+mx2+nx+p=(x-1)(x+4)(x+k)=x3+(k+3)x2+(3k-4)x-4k,
∴$\left\{\begin{array}{l}{m=k+3}\\{n=3k-4}\\{p=-4k}\end{array}\right.$,
∴2m-2n-p+86=2(k+3)-2(3k-4)+4k+86
=2k+6-6k+8+4k+86
=100,
故答案为:100.
点评 本题主要考查因式分解的意义,根据系数设另一个因式,从而变形将待求式子的未知数化为统一未知数是解题的关键.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
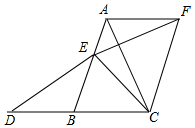 如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.
如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
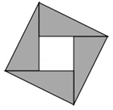 如图是“赵爽弦图”,由4个全等的直角三角形拼成的图形,若大正方形的面积是13,小正方形的面积是1,设直角三角形较长直角边为a,较短直角边为b,则a+b的值是5.
如图是“赵爽弦图”,由4个全等的直角三角形拼成的图形,若大正方形的面积是13,小正方形的面积是1,设直角三角形较长直角边为a,较短直角边为b,则a+b的值是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下面是某地区近5年城镇居民与农村居民人均收入增速对比表:
下面是某地区近5年城镇居民与农村居民人均收入增速对比表:| 年份 增速 类别 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 城镇 | 8.5 | 13.6 | 12.5 | 9.3 | 11.5 |
| 农村 | 10 | 10.5 | 14.2 | 12.5 | 14.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com