
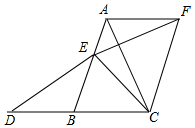
 如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.
如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.分析 (1)利用旋转的性质得AC=BC,∠BCA=60°,则可判断△ABC为等边三角形,过点E做EG∥AC交BC于点G,如图,则△EBG为等边三角形,所以EG=BE=BG,∠EBG=∠EGB=60°,则∠EBD=∠EGC=120°,接下来证明△BDE≌△GCE得到BD=GC,然后利用等线段代换可得到AE=DB;
(2)利用BD=AE,BE=BC=CE=EF等线段代换易得四对线段,使每对线段长度之和等于AB的长.
解答 解:(1)∵△BCE绕点C顺时针旋转60°至△ACF,
∴AC=BC,∠BCA=60°,
∴△ABC为等边三角形,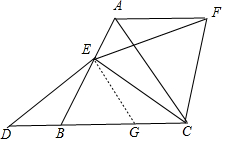
过点E做EG∥AC交BC于点G,如图,
∴△EBG为等边三角形,
∴EG=BE=BG,∠EBG=∠EGB=60°,
∴∠EBD=∠EGC=120°,
∵ED=EC
∴∠D=∠ECD,
在△BDE和△GCE中
$\left\{\begin{array}{l}{∠EBD=∠EGC}\\{∠D=∠GCE}\\{ED=EC}\end{array}\right.$,
∴△BDE≌△GCE,
∴BD=GC,
∵△ABC为等边三角形,
∴AB=BC,
∴AB-BE=BC-BG,
∴AE=CG,
∴AE=DB;
(2)AE+BE=AB;BD+BE=AB;AE+AF=AB;BD+AF=AB.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
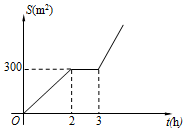 某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.
某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com