
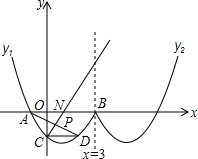
 ��ͼ������y1�����ߵ�һ���֣��ұ���ʽΪ��y1=$\frac{\sqrt{3}}{3}$��x2-2x-3����x��3������y2������y1����ֱ��x=3�Գƣ�
��ͼ������y1�����ߵ�һ���֣��ұ���ʽΪ��y1=$\frac{\sqrt{3}}{3}$��x2-2x-3����x��3������y2������y1����ֱ��x=3�Գƣ����� ��1���Ե�A��B��C���������Ҫ���ף���A���B�Ƕ��κ��������Ľ��㣬��C������Ľ��㣬����x=3��������⣬���ǽ�y1=$\frac{{\sqrt{3}}}{3}��{x^2}-2x-3����x��3��$������ƽ�ƣ��Ӷ������������y2�Ľ���ʽ��
��2��Ҫ���⣬ֻ�е�CM��ֱƽ��ADʱ��������y2�ҵ���M���ʵ�M��Ϊֱ�ߣ�C��AD���е�P���ߣ��Ľ��㣻
��3����ȻMN��ֵ�̶�������y2�ϵĵ㣬��CM�ľ������ĵ㣬����CMƽ�е�ֱ����y2ֻ��һ������ʱ����Ϊ����
��� �⣺��1����y1=$\frac{\sqrt{3}}{3}$��x2-2x-3���У���y1=0������0=$\frac{\sqrt{3}}{3}$��x2-2x-3�������x=-1��x=3��
��A��-1��0����B��3��0����
�֡�CΪ��y��Ľ��㣬
��C��0��-$\sqrt{3}$����
������y2������y1����ֱ��x=3�Գƣ�
������y2��������y1����ƽ��4����λ�õ���
��y2=$\frac{{\sqrt{3}}}{3}��{x^2}-10x+21��$��x��3����
��2����AD��ֱƽ��CM�����֪CDMAΪ���Σ���ʱ��M��1��0������Ȼ����y2�ϣ�
��ֱ��CM��ֱƽ��AD��ȡAD�е�P������������Ϊ��$\frac{1}{2}$��-$\frac{{\sqrt{3}}}{2}$����
��ֱ��CN�Ľ���ʽΪ��yCN=$\sqrt{3}x-\sqrt{3}$��
������y2�Ľ������꣺$\left\{\begin{array}{l}y=\sqrt{3}x-\sqrt{3}\\ y=\frac{{\sqrt{3}}}{3}��{x^2}-10x+21��\end{array}$��
��ã�x1=$\frac{{13+\sqrt{73}}}{2}$��x2=$\frac{{13-\sqrt{73}}}{2}$��������ȥ����
��x=$\frac{{13+\sqrt{73}}}{2}$��
��3����ΪMN�ij��ȹ̶����ʵ�P��MN�ľ������ʱ����PMN��������
�������һֱ��y=$\sqrt{3}$x+b��y2�ཻ�ڵ�P������Ȼ����ֻ��һ������ʱ������������
����$\left\{\begin{array}{l}y=\sqrt{3}x+b\\ y=\frac{{\sqrt{3}}}{3}��{x^2}-10x+21��\end{array}$ֻ��Ψһһ�����ʱ���������ǵ�P��
������$\sqrt{3}$x+b=$\frac{\sqrt{3}}{3}$��x2-10x+21����Ψһһ���⣬
��ã�x=$\frac{13}{2}$��
��x=$\frac{13}{2}$����y2=$\frac{{\sqrt{3}}}{3}��{x^2}-10x+21��$�����y=-$\frac{{7\sqrt{3}}}{12}$
�ʵ�P������Ϊ$��\frac{13}{2}��-\frac{{7\sqrt{3}}}{12}��$��
���� ������Ҫ������κ������ۺ�Ӧ�ã��漰���κ�����һԪ���η��̵Ĺ�ϵ��ͼ���ƽ�ơ����ε����ʵ�֪ʶ�㣮�ڣ�1����ȷ��������y2��������y1������ƽ��3����λ�õ��ǽ���Ĺؼ����ڣ�2����ȷ����ֱ��CM��ֱƽ��AD�ǽ���Ĺؼ����ڣ�3����ȷ����P���λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ����ʽ�ǿ���ѶȽϴ�


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+3��2=1 | B�� | ��x-3��2=1 | C�� | ��x+3��2=19 | D�� | ��x-3��2=19 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��a-2�� | B�� | a��a+2�� | C�� | a��a2-2�� | D�� | a��2-a�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
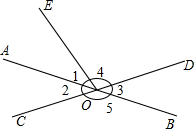 ��ͼ��ֱ��AB��CD�����O����1=��2��
��ͼ��ֱ��AB��CD�����O����1=��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
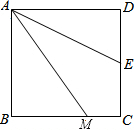 �������龳��
�������龳���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com