
【题目】如图,点E在正方形ABCD对角线AC上,且EC=2.5AE,直角三角形FEG的两直角边EF,EG分别交BC,CD于M,N.若正方形边长是a,则重叠部分四边形EMCN的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:过E作EP⊥BC于点P,EQ⊥CD于点Q,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵△FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,
在△EPM和△EQN中,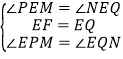 ,
,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM ,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为a,
∴AC=![]() =
=![]() a,
a,
∵EC=2.5AE,
∴EC=![]() a,
a,
∴正方形PCQE的面积=![]() ×(
×(![]() a)2=
a)2=![]() a2 ,
a2 ,
∴四边形EMCN的面积=![]() a2 .
a2 .
故选:A.
过E作EP⊥BC于点P,EQ⊥CD于点Q,△EPM≌△EQN,利用四边形EMCN的面积等于正方形PCQE的面积求解.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】定义:数x、y、z中较大的数称为max{x,y,z}.例如max{﹣3,1,﹣2}=1,函数y=max{﹣t+4,t,![]() }表示对于给定的t的值,代数式﹣t+4,t,
}表示对于给定的t的值,代数式﹣t+4,t,![]() 中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t= 时函数y的值最小.
中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t= 时函数y的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k为常数,且k≠5)经过点A(1,3).
(k为常数,且k≠5)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.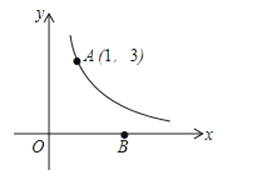
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式按字母x的降幂排列的是( )
A.﹣5x2﹣x2+2x2
B.ax3﹣2bx+cx2
C.﹣x2y﹣2xy2+y2
D.x2y﹣3xy2+x3﹣2y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,4),点B为直线x=1上的动点,设B(-1,y).

(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大美山水“硒都恩施”是一张亮丽的名片,八方游客慕名而来,今年“五一”期间,恩施州共接待游客1450000人,将1450000用科学记数法表示为( )
A.0.145×106B.14.5×105C.1.45×105D.1.45×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com