练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．（$\sqrt{3}$+$\sqrt{2}$）2005•（$\sqrt{3}$-$\sqrt{2}$）2006=$\sqrt{3}$-$\sqrt{2}$．

    分析 先根据积的乘方得到原式=[（$\sqrt{3}$+$\sqrt{2}$）•（$\sqrt{3}$-$\sqrt{2}$）]2005•（$\sqrt{3}$-$\sqrt{2}$），然后利用平方差公式计算．

    解答 解：原式=[（$\sqrt{3}$+$\sqrt{2}$）•（$\sqrt{3}$-$\sqrt{2}$）]2005•（$\sqrt{3}$-$\sqrt{2}$）
    =（3-2）2005•（$\sqrt{3}$-$\sqrt{2}$）
    =$\sqrt{3}$-$\sqrt{2}$．
    故答案为$\sqrt{3}$-$\sqrt{2}$．

    点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．对于一个数N可写成a×10n的形式，其中1≤|a|＜10，n是整数，像这样的记数法叫做科学记数法．在这种表示法中，a是整数位数只有1位的数，若|N|＞1，则n等于原数的整数位数减1；若|N|＜1，则n等于第一个非0数字前面0的个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．因式分解：-（a-b）mn-a+b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程组：$\left\{\begin{array}{l}{x：y=2：3}\\{5x-2y=8}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知Rt△ABC中，两直角边的和为14cm，斜边长为12cm，则这个直角三角形的面积为13．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．小骏考小苗解方程$\frac{0.1x-0.2}{0.02}$-$\frac{x+1}{0.3}$=3，小苗思考片刻后解答如下：
    解：原方程可化为$\frac{10x-20}{2}$-$\frac{10x+10}{5}$=3
    即5x-10-2x-2=3
    移项，的5x-2x=3+10+2
    合并同类项，得3x=15
    系数化为1，得x=5
    小苗的解法正确吗？你会解方程$\frac{2x}{0.3}$-$\frac{x-3}{0.5}$=0.4吗？试试看．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若max{a，b}表示a，b中的较大者，例如：max{3，2}=3，则函数y=max{x2，6-x}的最小值是$\frac{23}{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

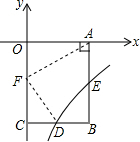    5．如图，已知B（4，-6），BA⊥x轴于点A，BC⊥y轴于点C，双曲线y=$\frac{k}{x}$（x＞0）经过BC的中点D，且与AB交于点E．
    （1）求反比例函数的解析式；
    （2）若点F是OC上一点，且△FDC∽△AFO，求经过E，F两点的一次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，抛物线y=x2+2x-3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．连接BC，AC，△ABC的外接圆记为⊙M，点D是⊙M与y轴的另一个交点．

    （1）求出点A，B，C的坐标；
    （2）求证：$\widehat{AD}=\widehat{BC}$；
    （3）求⊙M的半径；
    （4）如图，点P为⊙M上的一个动点，问：当点P的坐标是（-$\frac{\sqrt{10}+1}{2}$，-$\frac{\sqrt{10}+1}{2}$，以A，B，C，P为顶点的四边形有最大面积，最大面积是$\frac{3\sqrt{10}+6}{2}$（请直接填写答案在横线上）

    查看答案和解析>>

    同步练习册答案