
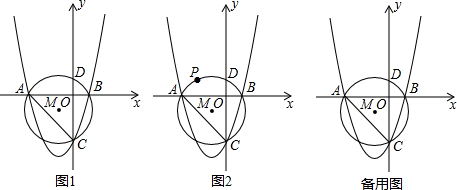
分析 (1)在y=x2+2x-3中令y=0,解方程求得x即可求得A和B的横坐标,在y=x2+2x-3中令x=0求得C的纵坐标;
(2)根据(1)可得AB=CD,然后根据同圆中,弦相等,则对应的弧相等,从而证得;
(3)易证△MBC是等腰直角三角形,利用三角函数即可求解;
(4)当P在弧AC上,且到AC的距离最远,即是AC弧的中点时,四边形的面积最大,求得P的坐标,即可求得四边形的面积.
解答 解(1)当x=0时,y=-3,
∴C(0,-3),
当y=0时,x2+2x-3=0,
解得:x1=1,x2=-3,
∴A(-3,0),B(1,0);
(2)∵A(-3,0),C(-3,0),
∴AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
∴$\widehat{AD}=\widehat{BC}$;
(3)连接MB和MC.
∵∠OAC=45°,∠CMB=90°,
连接MC,MB,在等腰直角三角形MBC中,
BC=$\sqrt{O{C^2}+O{B^2}}=\sqrt{{3^2}+{1^2}}=\sqrt{10}$,
∴r=$\sqrt{5}$;
(4)∵AB=4,
AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=3$\sqrt{2}$,BC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
其中AC最长.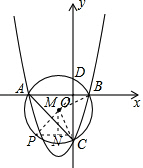
∴当P在弧AC上,且到AC的距离最远,即是AC弧的中点时,四边形的面积最大.
作MN∥y轴,作PN⊥MN于点N.
在直角△MNP中,MN=PN=PM•sin45°=$\sqrt{5}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{10}}{2}$.
则P的坐标是(-$\frac{\sqrt{10}}{2}$-$\frac{1}{2}$,-$\frac{\sqrt{10}}{2}$-$\frac{1}{2}$)即(-$\frac{\sqrt{10}+1}{2}$,-$\frac{\sqrt{10}+1}{2}$).
S△MAP=$\frac{1}{2}$×3×$\frac{\sqrt{10}+1}{2}$=$\frac{3(\sqrt{10}+1)}{4}$,
S△MPC=$\frac{1}{2}$×3×$\frac{\sqrt{10}+1}{2}$=$\frac{3(\sqrt{10}+1)}{4}$,
S△MBC=$\frac{1}{2}$×1×3=$\frac{3}{2}$.
则S四边形ABCP=$\frac{3(\sqrt{10}+1)}{2}$+$\frac{3}{2}$=$\frac{3\sqrt{10}+6}{2}$.
故答案是:(-$\frac{\sqrt{10}+1}{2}$,-$\frac{\sqrt{10}+1}{2}$),$\frac{3\sqrt{10}+6}{2}$.
点评 本题是二次函数与三角函数以及三角形的面积的综合应用,注意到P点的位置,正确求得P的坐标是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}-2\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}-\sqrt{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
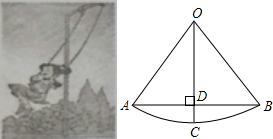 如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.
如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
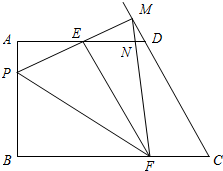 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是上底AD的中点,P是腰AB上一动点,联结PE并延长,交射线CD于点M,作EF⊥PE,交下底BC于点F,联结MF交AD于点N,联结PF,AB=AD=4,BC=6,点A、P之间的距离为x,△PEF的面积为y.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是上底AD的中点,P是腰AB上一动点,联结PE并延长,交射线CD于点M,作EF⊥PE,交下底BC于点F,联结MF交AD于点N,联结PF,AB=AD=4,BC=6,点A、P之间的距离为x,△PEF的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
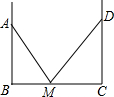 如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)
如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com