
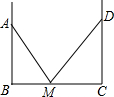
 如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)
如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947) 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
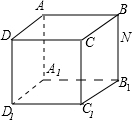 如图是一个棱长为4cm的正方体盒子,且蚂蚁在正方体盒子的内部D1C1的中点M处.它爬到BB1的中点N的最短路线长是2$\sqrt{10}$cm.
如图是一个棱长为4cm的正方体盒子,且蚂蚁在正方体盒子的内部D1C1的中点M处.它爬到BB1的中点N的最短路线长是2$\sqrt{10}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 制作桌面 | 制作桌脚 | |
| 1立方米木材 | ||
| X立方米木材 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com