
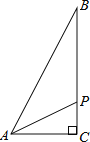
【题目】在![]() 中,
中,![]() ,点P从点A出发,以
,点P从点A出发,以![]() 的速度沿折线
的速度沿折线![]() 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为![]() ,线段AP的长度为
,线段AP的长度为![]() ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是![]()
A. 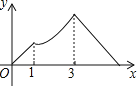 B.
B. 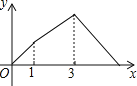
C. 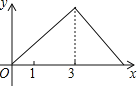 D.
D. 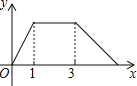
【答案】A
【解析】分析:这是分段函数:①点P在AC边上时,y=x,它的图象是一次函数图象的一部分;
②点P在边BC上时,利用勾股定理求得y与x的函数关系式,根据关系式选择图象;
③点P在边AB上时,利用线段间的和差关系求得y与x的函数关系式,由关系式选择图象.
详解:①当点P在AC边上,即0≤x≤1时,y=x,它的图象是一次函数图象的一部分;
②点P在边BC上,即1<x≤3时,根据勾股定理得: AP=![]() ,即y=
,即y=![]() ,则其函数图象是y随x的增大而增大,且不是一次函数.故B、C、D错误;
,则其函数图象是y随x的增大而增大,且不是一次函数.故B、C、D错误;
③点P在边AB上,即3<x≤3+![]() 时,y=
时,y=![]() +3﹣x=﹣x+3+
+3﹣x=﹣x+3+![]() ,其函数图象是直线的一部分.
,其函数图象是直线的一部分.
综上所述:A选项符合题意.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
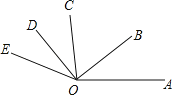
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:射线OP∥AE
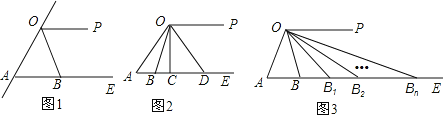
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn﹣1OP的角平分线OBn,其中点B,B1,B2,…,Bn﹣1,Bn都在射线AE上,试求∠ABnO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,![]() ,点E,F分别在BC、CD上,
,点E,F分别在BC、CD上,![]() ,试探究
,试探究![]() 面积的最小值。
面积的最小值。
下面是小丽的探究过程:
(1)延长EB至G,使![]() ,连接AG,可以证明
,连接AG,可以证明![]() .请完成她的证明;
.请完成她的证明;
(2)设![]() ,
,![]() ,
,![]()
①结合(1)中结论,通过计算得到![]() 与x的部分对应值。请求出表格中a的值:(写出解答过程)
与x的部分对应值。请求出表格中a的值:(写出解答过程)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
②利用上表和(1)中的结论通过描点、连线可以分别画出函数![]() 、
、![]() 的图像、请在图②中完善她的画图;
的图像、请在图②中完善她的画图;
③根据以上探究,估计![]() 面积的最小值约为(结果估计到0.1)。
面积的最小值约为(结果估计到0.1)。
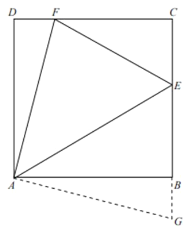
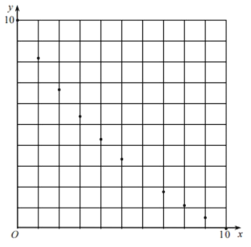
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
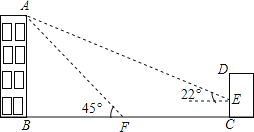
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )

A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点M是AC的中点,以AB为直径作
,点M是AC的中点,以AB为直径作![]() 分别交
分别交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 填空:
填空:
![]() 若
若![]() ,当
,当![]() 时,
时,![]() ______;
______;
![]() 连接
连接![]() ,当
,当![]() 的度数为______时,四边形ODME是菱形.
的度数为______时,四边形ODME是菱形.
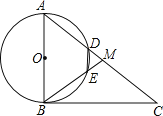
查看答案和解析>>
科目:初中数学 来源: 题型:
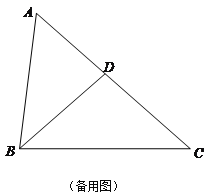
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上一点,且
,D是AC边上一点,且![]() ,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),
,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),![]() ,AE与BD相交于点G.
,AE与BD相交于点G.
(1)求证:BD平分![]() ;
;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)联结FG,当![]() 是等腰三角形时,求BE的长度.
是等腰三角形时,求BE的长度.
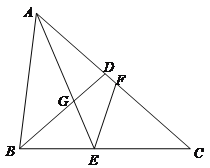
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=![]() (
(![]() 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含![]() 的代数式表示);
的代数式表示);
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com