
【题目】已知:射线OP∥AE
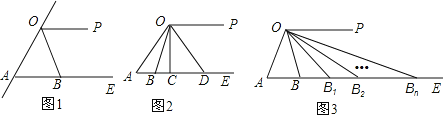
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn﹣1OP的角平分线OBn,其中点B,B1,B2,…,Bn﹣1,Bn都在射线AE上,试求∠ABnO的度数.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
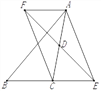
【题目】如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.
(1)求证:AF=CE;
(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
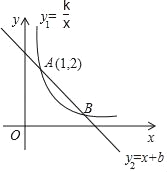
【题目】反比例函数y1=![]() (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
![]()
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值;
(2)①若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.
②此时,若数轴上存在一点E,使得AE=2CE,求点E所对应的数(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以6个单位长度/秒的速度同时从O点向左运动.当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
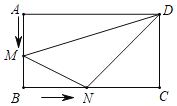
【题目】如图,在长方形![]() 中,
中,![]() 长为3,
长为3,![]() 长为6,点
长为6,点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 以每秒1个单位的速度运动,同时点
以每秒1个单位的速度运动,同时点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 以每秒2个单位的速度运动(当一个点到达终点时另一个点也随之停止运动).若运动的时间为
以每秒2个单位的速度运动(当一个点到达终点时另一个点也随之停止运动).若运动的时间为![]() 秒,则三角形
秒,则三角形![]() 的面积为______(用含
的面积为______(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点P从点A出发,以
,点P从点A出发,以![]() 的速度沿折线
的速度沿折线![]() 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为![]() ,线段AP的长度为
,线段AP的长度为![]() ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是![]()
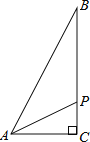
A. 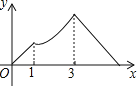 B.
B. 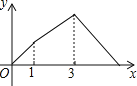
C. 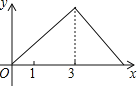 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,现将A、B之间的距离记作|AB|,定义|AB|=|a﹣b|.
(1)求2019b+a的值;
(2)求|AB|的值;
(3)设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com