
【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以6个单位长度/秒的速度同时从O点向左运动.当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
【答案】(1)点P对应的数是1;(2)存在x的值,当x=﹣3或5时,满足点P到点A、点B的距离之和为8;(3)当点A与点B之间的距离为3个单位长度时,点P所对应的数是﹣4或﹣28.
【解析】
(1)由点P到点A、点B的距离相等得点P是线段AB的中点,而A、B对应的数分别为﹣1、3,根据数轴即可确定点P对应的数;
(2)分两种情况讨论,①当点P在A左边时,②当点P在B点右边时,分别求出x的值即可.
(3)分两种情况讨论,①当点A在点B左边,两点相距3个单位时,②当点A在点B右边,两点相距3个单位时,分别求出t的值,然后求出点P对应的数即可.
(1)∵点P到点A、点B的距离相等,∴点P是线段AB的中点.
∵点A、B对应的数分别为﹣1、3,∴点P对应的数是1;
(2)①当点P在A左边时,﹣1﹣x+3﹣x=8,解得:x=﹣3;
②当点P在B点右边时,x﹣3+x﹣(﹣1)=8,解得:x=5.
即存在x的值,当x=﹣3或5时,满足点P到点A、点B的距离之和为8;
(3)①当点A在点B左边,两点相距3个单位时,此时需要的时间为t,则3+0.5t﹣(2t﹣1)=3,解得:t=![]() ,则点P对应的数为﹣6×
,则点P对应的数为﹣6×![]() =﹣4;
=﹣4;
②当点A在点B右边,两点相距3个单位时,此时需要的时间为t,则2t﹣1﹣(3+0.5t)=3,1.5t=7,解得:t=![]() ,则点P对应的数为﹣6×
,则点P对应的数为﹣6×![]() =﹣28.
=﹣28.
综上可得:当点A与点B之间的距离为3个单位长度时,点P所对应的数是﹣4或﹣28.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B分别在y轴和x轴上,∠ABO=60°,在坐标轴上找一点P,使得△PAB是等腰三角形,则符合条件的点P共有( )
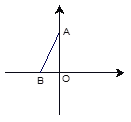
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足![]()
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A、B两种上网学习的月收费方案:
A方案:月租7元,可上网25小时,若超时,超出部分按每分钟0.01元收费;
B方案:月租10元,可上网50小时,若超时,超出部分按每分钟0.01元收费;
设每月上网学习时间为![]() 小时.
小时.
(1)当![]() >50时,用含有x的代数式分别表示A、B两种上网的费用;
>50时,用含有x的代数式分别表示A、B两种上网的费用;
(2)当x=100时,分别求出两种上网学习的费用.
(3)若上网40小时,选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-1,1,2这三个数字中,随机抽取一个数记为a,那么,使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为![]() ,且使关于x的不等式组
,且使关于x的不等式组![]() 有解的概率为________.
有解的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com