
【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
![]()
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值;
(2)①若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.
②此时,若数轴上存在一点E,使得AE=2CE,求点E所对应的数(直接写出答案).
【答案】(1)A点对应的数为-2;D点对应的数为3;C点对应的数为4;p=5;(2)①15;②-9或-17.
【解析】
(1)根据以B为原点,则A,D,C所对应的数分别为:-2,3,4,进而得到p的值;
(2)①用x的代数式分别表示A,B,D,C所对应的数,根据题意列方程解答即可;②根据题意可知A表示的数为-21, C点表示的数为-15,然后分情况讨论E的位置求解即可.
(1)解:∵B为原点,AB=2,则A点对应的数为-2;BD=3,则D点对应的数为3;DC=1,则C点对应的数为3+1=4,则P=-2+3+4=5.
(2)解: ①由题意,A,B,D,C表示的数分别为:-6-x,-4-x,-1-x,-x,
则:-6-x-4-x-1-x-x=-71,
解得:x=15;
②由上题知:A表示的数为-15-6=-21, C点表示的数为-15,
1)当E在AC之间时,如下图

∵AC=-15-(-21)=6,且AE=2CE,
解得CE=2,
∴此时E点表示的数为-17;
2)当E在C的右边时,如下图

∵AC=-15-(-21)=6,且AE=2CE,
解得CE=6,
∴此时E点表示的数为-9,
综上:点E所对应的数为-9或-17.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
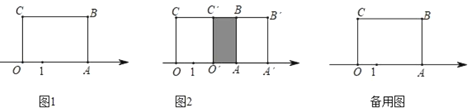
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为 .
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为OABC,移动后的长方形OABC与原长方形OABC重叠部分(如图8中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A表示的数是 .
②设点A的移动距离AA'=x
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA的中点,点E在找段OO'上,且OO'=3OE,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
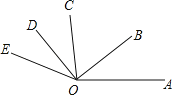
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
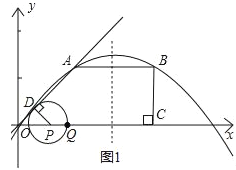
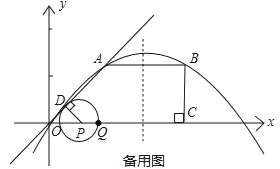
【题目】如图,O是平面直角坐标系的原点.在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,1),B(3,1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.设P点运动的时间为t秒(0<t<2).
(1)求经过O、A、B三点的抛物线的解析式;
(2)过P作PD⊥OA于D,以点P为圆心,PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q.
①则P点的坐标为_____,Q点的坐标为_____;(用含t的代数式表示)
②试求t为何值时,⊙P与四边形OABC的两边同时相切;
③设△OPD与四边形OABC重叠的面积为S,请直接写出S与t的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC=8![]() ,BD=6
,BD=6![]() ,且
,且![]() ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:射线OP∥AE
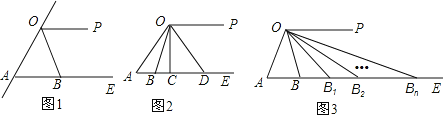
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn﹣1OP的角平分线OBn,其中点B,B1,B2,…,Bn﹣1,Bn都在射线AE上,试求∠ABnO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
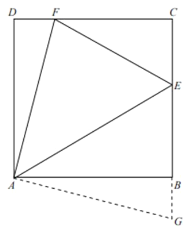
【题目】如图①,在正方形ABCD中,![]() ,点E,F分别在BC、CD上,
,点E,F分别在BC、CD上,![]() ,试探究
,试探究![]() 面积的最小值。
面积的最小值。
下面是小丽的探究过程:
(1)延长EB至G,使![]() ,连接AG,可以证明
,连接AG,可以证明![]() .请完成她的证明;
.请完成她的证明;
(2)设![]() ,
,![]() ,
,![]()
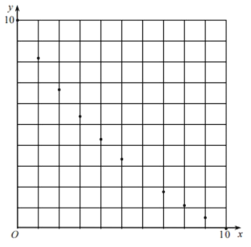
①结合(1)中结论,通过计算得到![]() 与x的部分对应值。请求出表格中a的值:(写出解答过程)
与x的部分对应值。请求出表格中a的值:(写出解答过程)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
②利用上表和(1)中的结论通过描点、连线可以分别画出函数![]() 、
、![]() 的图像、请在图②中完善她的画图;
的图像、请在图②中完善她的画图;
③根据以上探究,估计![]() 面积的最小值约为(结果估计到0.1)。
面积的最小值约为(结果估计到0.1)。
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
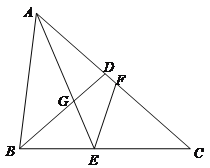
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上一点,且
,D是AC边上一点,且![]() ,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),
,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),![]() ,AE与BD相交于点G.
,AE与BD相交于点G.
(1)求证:BD平分![]() ;
;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)联结FG,当![]() 是等腰三角形时,求BE的长度.
是等腰三角形时,求BE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com