
如图,在矩形ABCD中,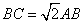 ,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
①∠AEB=∠AEH ②DH=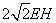 ③
③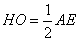 ④
④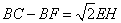
其中正确命题的序号是 (填上所有正确命题的序号).
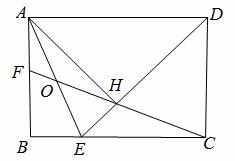
①③.
【考点】矩形的性质;等腰(直角)三角形的判定和性质;三角形内角和定理;全等三角形的判定和性质;直角三角形斜边上的中线的判定;勾股定理;相似三角形的判定和性质;特殊元素法和方程思想的应用.
【分析】①∵在矩形ABCD中,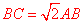 ,∴不妨设
,∴不妨设 ,则
,则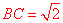 .
.
∵∠ADC的平分线交边BC于点E,∴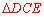 是等腰直角三角形.∴
是等腰直角三角形.∴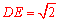 .
.
∴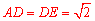 .∴
.∴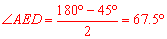 .
.
∴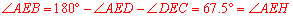 .故命题①正确.
.故命题①正确.
②∵ 是等腰直角三角形,∴
是等腰直角三角形,∴ .
.
∵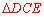 是等腰直角三角形,∴
是等腰直角三角形,∴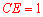 .∴
.∴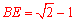 .
.
不难证明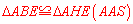 ,∴
,∴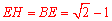 .∴
.∴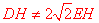 .故命题②错误.
.故命题②错误.
③∵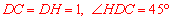 ,∴
,∴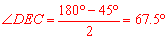 .∴
.∴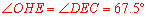 。
。
∵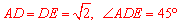 ,∴
,∴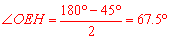 .
.
∴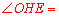
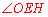 .∴
.∴ 是
是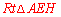 斜边上的中线.∴
斜边上的中线.∴ .故命题③正确.
.故命题③正确.
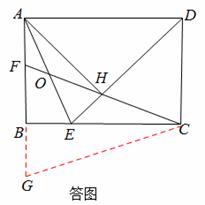 ④如答图,延长AB至G,使BG=BF,连接CG,
④如答图,延长AB至G,使BG=BF,连接CG,
在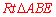 中,
中,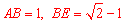 ,
,
∴根据勾股定理得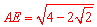 .
.
设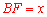 ,则
,则 .
.
在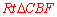 中,根据勾股定理得
中,根据勾股定理得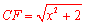 .
.
易证明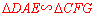 ,∴
,∴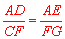 .
.
∴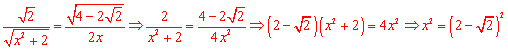 .
.
∴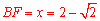 .
.
∴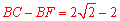 .
.
又∵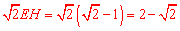 .
.
∴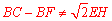 .故命题④错误.
.故命题④错误.
综上所述,正确命题的序号是①③.


科目:初中数学 来源: 题型:
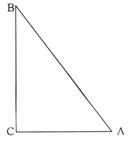
如图,Rt△ABC.中,∠C=90O。
(1) 用尺规作图作Rt△ABC的重心(三边中线的交点)P.(保留作图痕迹,不要求
写作法、证明);
(2) 你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心(外接圆圆心)之间的距离?并请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
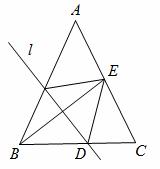
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线 翻折后,点B落在边AC的中点E处,直线
翻折后,点B落在边AC的中点E处,直线 与边BC交于点D,那么BD的长为【 】
与边BC交于点D,那么BD的长为【 】
A.13 B.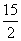 C.
C.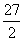 D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
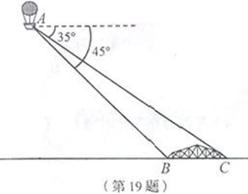
小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°
和35°,已知大桥BC与地面在同一水平面上,其长度为100m。请求出热气球离地面的高度。
(结果保留整数,参考数据: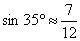 ,
, 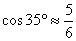 ,
,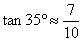
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com