
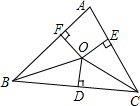
 如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )
如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )| A、70° | B、120° |
| C、125° | D、130° |
| 1 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC,AB交x轴于点F.
如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC,AB交x轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 | 购买数量 (台) | 原价购买总额(元) | 政府补贴返还比例 | 补贴返还总金额(元) | 每台补贴返还金额(元) |
| 冰箱 | 40000 | 13% | |||
| 电视机 | x | 15000 | 13% |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线AC与x轴、y轴分别交于点C(-2,0)、A(0,4),B点坐标为(4,0),过点B作BD⊥AC于D,BD交OA于点H.
如图,直线AC与x轴、y轴分别交于点C(-2,0)、A(0,4),B点坐标为(4,0),过点B作BD⊥AC于D,BD交OA于点H.| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
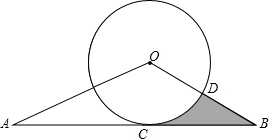 如图,已知△AOB与⊙O相切于点C,边OB与⊙O 相交于点D,OD=BD且SinA=
如图,已知△AOB与⊙O相切于点C,边OB与⊙O 相交于点D,OD=BD且SinA=| 2 |
| 5 |
| 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com