
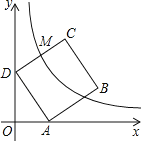
【题目】如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函y=![]() 经过CD的中点M,那么k=_____.
经过CD的中点M,那么k=_____.
【答案】![]() +6
+6
【解析】
先根据△CDE≌△DAO,得到DE=AO=2,DO=2![]() =CE,再根据F是CE的中点,即可得到F(
=CE,再根据F是CE的中点,即可得到F(![]() ,2+2
,2+2![]() ),最后根据反比例函数y=
),最后根据反比例函数y=![]() 的图象过CE的中点F,即可得到k的值.
的图象过CE的中点F,即可得到k的值.
解:如图,作CE⊥y轴于点E.
∵正方形ABCD的顶点A、D分别在x轴、y轴上,
∴∠CED=∠DOA=90°,∠DCE=∠ADO,CD=DA,
∴△CDE≌△DAO(AAS),
∴DE=AO=2,
又∵∠ODA=30°,
∴Rt△AOD中,AD=2AO=4,DO=2![]() =CE,
=CE,
∴EO=2+2![]() ,
,
∴C(2![]() ,2+2
,2+2![]() ),D(0,2
),D(0,2![]() ),
),
∵M是CD的中点,
∴M(![]() ,1+2
,1+2![]() ),
),
∵反比例函y=![]() 经过CD的中点M,
经过CD的中点M,
∴k=![]() (1+2
(1+2![]() )=
)=![]() +6,
+6,
故答案为:![]() +6.
+6.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
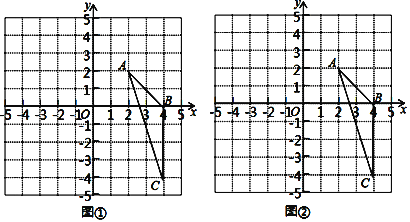
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)将△ABC绕点A顺时针旋转90°后得到△AB1C1,在图①中画出△AB1C1,并求出在旋转过程中△ABC扫过的面积;
(2)在图②中以点O为位似中心,将△ABC缩小为原来的![]() ,并写出点C的对应点的坐标.
,并写出点C的对应点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
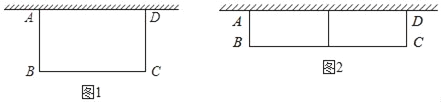
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
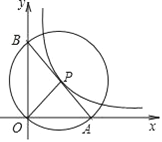
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
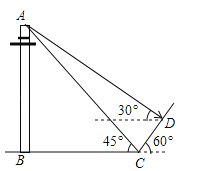
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,若已知
,若已知![]() 点的坐标为
点的坐标为![]() .
.
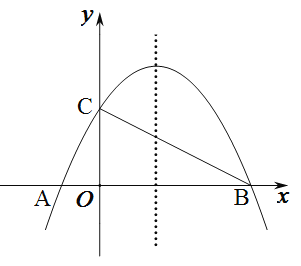
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点![]() ,使
,使![]() 的周长最小,求出点
的周长最小,求出点![]() 的坐标;
的坐标;
(3)在第一象限的抛物线上是否存在点![]() ,使
,使![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+3x+2的图象如图1所示,根据图象回答问题:
(1)当x满足 时,x2+3x+2>0;
(2)在解决上述问题的基础上,探究解决新问题:
①函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
②下表是函数y=![]() 的几组y与x的对应值.
的几组y与x的对应值.
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477 … | 4.472 … | 2.449 … | 1.414 … | 0 | 0 | 1.414 … | 2.449 … | 4.472 … | 5.477 … | … |
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
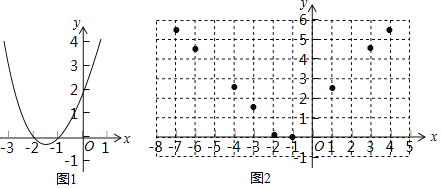
③利用图象,直接写出关于x的方程x4=x2+3x+2的所有近似实数解 (结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在将式子![]() (m>0)化简时,
(m>0)化简时,
小明的方法是:![]() =
=![]() =
=![]() =
=![]() ;
;
小亮的方法是: ![]() ;
;
小丽的方法是:![]() .
.
则下列说法正确的是( )
A. 小明、小亮的方法正确,小丽的方法不正确
B. 小明、小丽的方法正确,小亮的方法不正确
C. 小明、小亮、小丽的方法都正确
D. 小明、小丽、小亮的方法都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图所示,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B,C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内,且点A在点D的左侧.
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长p关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com