【题目】函数y＝x2+3x+2的图象如图1所示，根据图象回答问题：
（1）当x满足 时，x2+3x+2＞0；
（2）在解决上述问题的基础上，探究解决新问题：
①函数y＝
的自变量x的取值范围是 ；
②下表是函数y＝的几组y与x的对应值．
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477 … | 4.472 … | 2.449 … | 1.414 … | 0 | 0 | 1.414 … | 2.449 … | 4.472 … | 5.477 … | … |
如图2，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点的大概位置，请你根据描出的点，画出该函数的图象：
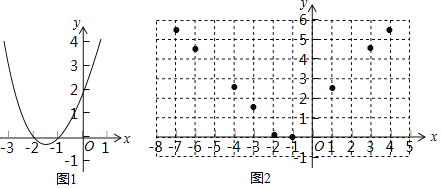
③利用图象，直接写出关于x的方程x4=x2+3x+2的所有近似实数解 （结果精确到0.1）
【答案】（1）x＜﹣2或x＞﹣1；（2）①x≤﹣2或x≥﹣1；②详见解析；③﹣0.8（﹣0.9～﹣0.6）和1.8（1.6～1.9）．
【解析】
（1）根据图象与x轴的交点坐标即可得结论；
（2）①根据（1）所得结论即可求解；
②根据平面直角坐标系中描出的点即可画出函数图象；
③结合图象可得出答案；
解：（1）观察图象可知：
y＞0，即图象在x轴的上方的部分，
所以x＜﹣2或x＞﹣1．
故答案为x＜﹣2或x＞﹣1．
（2）①根据（1）的结论可知：
自变量x的取值范围是x≤﹣2或x≥﹣1．
②如图即为画出的函数图象．
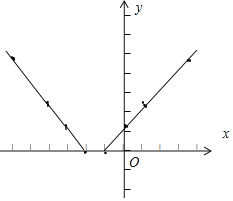
③根据所画的图象可知：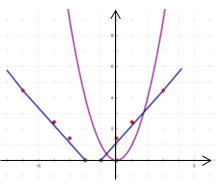
所求方程的解为y=
和
交点的横坐标
所以近似实数解为：-0.8（-0.9～-0.6）和1.8（1.6～1.9）．
故答案为-0.8（-0.9～-0.6）和1.8（1.6～1.9）．
科目：初中数学 来源： 题型：
【题目】给出如下定义：对于⊙O的弦MN和⊙O外一点P（M，O，N三点不共线，且点P，O在直线MN的异侧），当∠MPN+∠MON＝180°时，则称点P是线段MN关于点O的关联点．图1是点P为线段MN关于点O的关联点的示意图．
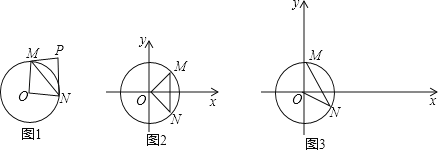
在平面直角坐标系xOy中，⊙O的半径为1．
（1）如图2，已知M（
，），N（，﹣），在A（1，0），B（1，1），C（
，0）三点中，是线段MN关于点O的关联点的是 ；
（2）如图3，M（0，1），N（
，﹣
），点D是线段MN关于点O的关联点．
①∠MDN的大小为 ；
②在第一象限内有一点E（
m，m），点E是线段MN关于点O的关联点，判断△MNE的形状，并直接写出点E的坐标；
③点F在直线y＝﹣
x+2上，当∠MFN≥∠MDN时，求点F的横坐标x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数的解析式是y＝﹣x2+2x+3．
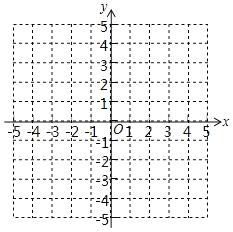
（1）用配方法将该二次函数化成y＝a（x﹣h）2+k的形式，并写出顶点坐标；
（2）在图中画出该二次函数的图象（不需要列表），并写出该图象与x轴的交点；
（3）当0≤x＜3时，直接写出y的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
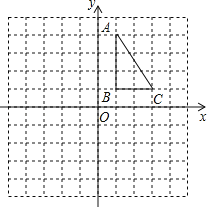
【题目】如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）画出△ABC绕点O逆时针旋转90°后的△A2B2C2；
（3）在（2）的条件下，求线段BC扫过的面积（结果保留π）．
查看答案和解析>>
科目：初中数学 来源： 题型：
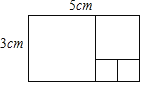
【题目】请将宽为3cm、长为ncm的长方形（n为正整数）分割成若干小正方形，要求小正方形的边长是正整数且个数最少．例如，当n＝5cm时，此长方形可分割成如右图的4个小正方形．
请回答下列问题：
（1）n＝16时，可分割成几个小正方形？
（2）当长方形被分割成20个小正方形时，求n所有可能的值；
（3）一般地，n＞3时，此长方形可分割成多少个小正方形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
