练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
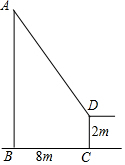
    16．如图，小华将升旗的绳子拉紧到旗杆底端点B，绳子末端刚好接触到地面，然后拉紧绳子使其末端到点D处，点D到地面的距离CD长为2m，点D到旗杆AB的水平距离为8m，若设旗杆的高度AB长为xm，则根据题意所列的方程是（　　）
    A．（x-2）2+82=x2B．（x+2）2+82=x2C．x2+82=（x-2）2D．x2+82=（x+2）2

    分析 直接利用勾股定理分析得出符合题意的等式．

    解答 解：过点D，作DE⊥AB于点E，
    由题意可得：AE2+DE2=AD2，
    ∵AB=x，则AE=x-2，
    则（x-2）2+82=x2．
    故选：A．

    点评 此题主要考查了勾股定理的应用，正确得出等式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

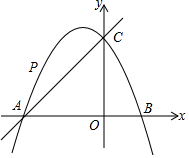    6．如图在平面直角坐标系中，抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B，与y轴交于点C，直线y=x+4经过A，C两点．
    （1）求抛物线的解析式；
    （2）在AC上方的抛物线上有一动点P，当点P运动到某位置时，以AP，AO为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，在平面直角坐标系中，抛物线y=-x2+$\frac{1}{4}$与y轴相交于点A，点B与点O关于点A对称．
    （1）填空：点B的坐标为（0，$\frac{1}{2}$）；
    （2）过点B的直线y=kx+b（其中k＜0）与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长（用含k的式子表示），并判断点P是否在抛物线上，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．用科学记数法表示2016000000时，正确的写法是（　　）
    A．2.016×1010B．2.016×109C．2016×106D．2016×1010

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某公司在2014年第一季度平均每月亏损1.5万元，第二季度平均每月盈利2.6万元，第三季度平均每月盈利1.7万元，第四季度平均每月亏损2.3万元．这个公司去年总的盈亏情况如何？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．在实数$\frac{22}{7}$，-$\sqrt{3}$，-3.14，0，π，2.1611 611 61…，$\root{3}{9}$中，无理数有（　　）
    A．1 个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，抛物线y=ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点．

    （1）求抛物线的解析式；
    （2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；
    （3）已知H（0，-1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF=BC，求点G的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知：y与x-3成正比例，且当x=-2时，y的值为10．
    （1）求y与x之间的函数关系式；
    （2）当x=2时，求y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列四个命题中，真命题有（　　）
    ①6的平方根是±$\sqrt{6}$
    ②三角形的一个外角大于任何一个内角
    ③一组数据与最小数据的差成为极差，它是刻画数据离散程度的一个统计量
    ④凡是定理都可以作为公理．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    同步练习册答案