

分析 (1)根据抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x-1,再根据OC=OA,AB=4,可得A(-3,0),最后代入抛物线y=ax2+2ax+3,得抛物线的解析式为y=-x2-2x+3;
(2)根据点M(m,0),可得矩形PQNM中,P(m,-m2-2m+3),Q(-2-m,-m2-2m+3),再根据矩形PQNM的周长=2(PM+PQ)=-2(m+2)2+10,可得当m=-2时,矩形PQNM的周长有最大值10,M的坐标为(-2,0),最后由直线AC为y=x+3,AM=1,求得E(-2,1),ME=1,据此求得△AEM的面积;
(3)连接CB并延长,交直线HG与Q,根据已知条件证明BC=BF=BQ,再根据C(0,3),B(1,0),得出Q(2,-3),根据H(0,-1),求得QH的解析式为y=-x-1,最后解方程组$\left\{\begin{array}{l}{y=-x-1}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,可得点G的坐标.
解答 解:(1)由抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x=-$\frac{2a}{2a}$=-1,
∵OC=OA,
∴A(-c,0),B(-2+c,0),
∵AB=4,
∴-2+c-(-c)=4,
∴c=3,
∴A(-3,0),
代入抛物线y=ax2+2ax+3,得
0=9a-6a+3,
解得a=-1,
∴抛物线的解析式为y=-x2-2x+3;
(2)如图1,∵M(m,0),PM⊥x轴,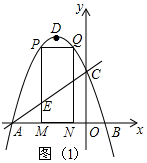
∴P(m,-m2-2m+3),
又∵对称轴为x=-1,PQ∥AB,
∴Q(-2-m,-m2-2m+3),
又∵QN⊥x轴,
∴矩形PQNM的周长
=2(PM+PQ)
=2[(-m2-2m+3)+(-2-m-m)]
=2(-m2-4m+1)
=-2(m+2)2+10,
∴当m=-2时,矩形PQNM的周长有最大值10,
此时,M(-2,0),
由A(-3,0),C(0,3),可得
直线AC为y=x+3,AM=1,
∴当x=-2时,y=1,即E(-2,1),ME=1,
∴△AEM的面积=$\frac{1}{2}$×AM×ME=$\frac{1}{2}$×1×1=$\frac{1}{2}$;
(3)如图2,连接CB并延长,交直线HG与Q,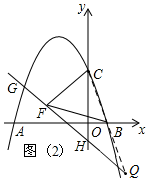
∵HG⊥CF,BC=BF,
∴∠BFC+∠BFQ=∠BCF+∠Q=90°,∠BFC=∠BCF,
∴∠BFQ=∠Q,
∴BC=BF=BQ,
又∵C(0,3),B(1,0),
∴Q(2,-3),
又∵H(0,-1),
∴QH的解析式为y=-x-1,
解方程组$\left\{\begin{array}{l}{y=-x-1}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,可得
$\left\{\begin{array}{l}{x=\frac{-1-\sqrt{17}}{2}}\\{y=\frac{\sqrt{17}-1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{17}}{2}}\\{y=\frac{-1-\sqrt{17}}{2}}\end{array}\right.$,
∴点G的坐标为($\frac{-1-\sqrt{17}}{2}$,$\frac{\sqrt{17}-1}{2}$)或($\frac{-1+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$).
点评 本题是二次函数综合题,主要考查了二次函数与直线交点的求法、矩形的性质、一元二次方程的解法、二次函数最值的求法.在求周长的最值时,要转化为二次函数最值问题进行解答,灵活运用二次函数的对称性,运用数形结合、方程思想是解答本题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:选择题
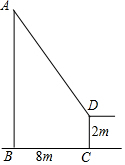 如图,小华将升旗的绳子拉紧到旗杆底端点B,绳子末端刚好接触到地面,然后拉紧绳子使其末端到点D处,点D到地面的距离CD长为2m,点D到旗杆AB的水平距离为8m,若设旗杆的高度AB长为xm,则根据题意所列的方程是( )
如图,小华将升旗的绳子拉紧到旗杆底端点B,绳子末端刚好接触到地面,然后拉紧绳子使其末端到点D处,点D到地面的距离CD长为2m,点D到旗杆AB的水平距离为8m,若设旗杆的高度AB长为xm,则根据题意所列的方程是( )| A. | (x-2)2+82=x2 | B. | (x+2)2+82=x2 | C. | x2+82=(x-2)2 | D. | x2+82=(x+2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边向点A以1厘米/秒的宽度移动;同时,点Q也从点B开始沿BC边向点C以2厘米/秒的速度移动,问几秒后,△PBQ的面积为36平方厘米?
如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边向点A以1厘米/秒的宽度移动;同时,点Q也从点B开始沿BC边向点C以2厘米/秒的速度移动,问几秒后,△PBQ的面积为36平方厘米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9的算术平方根是3 | B. | $\sqrt{16}$平方根是±2 | ||
| C. | 27的平方根是±3 | D. | 立方根等于-1的实数是-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 4个 | C. | 5 个 | D. | 9个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com