【题目】已知一个二次函数的对称轴是x＝1，图象最低点P的纵坐标是﹣8，图象过（﹣2，10）且与x轴交于A，B与y轴交于C．求：
（1）这个二次函数的解析式；
（2）△ABC的面积．
【答案】（1）y＝2（x﹣1）2﹣8；（2）12．
【解析】
（1）由于已知抛物线的顶点坐标，则可设顶点式y＝a（x﹣1）2﹣8，然后把（﹣2，10）代入求出a即可；
（2）根据坐标轴上点的坐标特征求出A、B、C三点坐标，然后利用三角形面积公式求解．
（1）设抛物线解析式为y＝a（x﹣1）2﹣8，
把（﹣2，10）代入得a（﹣2﹣1）2﹣8＝10，
解得：a＝2，
所以抛物线解析式为y＝2（x﹣1）2﹣8；
（2）当x＝0时，y＝2（x﹣1）2﹣8＝﹣6，则C（0，﹣6），
当y＝0时，2（x﹣1）2﹣8＝0，
解得x1＝﹣1，x2＝3，
则A（﹣1，0），B（3，0），
所以△ABC的面积＝
×（3+1）×6＝12．
科目：初中数学 来源： 题型：
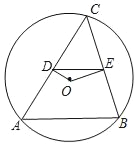
【题目】如图，在圆O中，弦AB＝8，点C在圆O上(C与A，B不重合)，连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E．
(1)求线段DE的长；
(2)点O到AB的距离为3，求圆O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝x2﹣2mx+m2+1（m为常数），当自变量x的值满足﹣3≤x≤﹣1时，与其对应的函数值y的最小值为5，则m的值为（ ）
A. 1或﹣3 B. ﹣3或﹣5 C. 1或﹣1 D. 1或﹣5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知：⊙O.
求作：⊙O的内接等腰直角三角形.
作法：如图，
①作直径AB；
②分别以点A，B为圆心，以大于
的同样长为半径作弧，两弧交于M，N两点；
③作直线MN交⊙O于点C，D；
④连接AC，BC．
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明.
证明：∵AB是直径， C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表给出了以下结论：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y＝ax2+bx+c有最小值，最小值为﹣3；②当﹣
＜x＜2时，y＜0；③二次函数y＝ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴的两侧；④当x＜1时，y随x的增大而减小．则其中正确结论有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
∥
，⊙O与和分别相切于点A和点B．点M和点N分别是和上的动点，MN沿和平移．⊙O的半径为1，∠1＝60°．下列结论错误的是（ ）
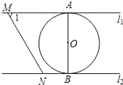
A. 
B. l1和l2的距离为2
C. 若∠MON＝90°，则MN与⊙O相切 D. 若MN与⊙O相切，则
查看答案和解析>>
科目：初中数学 来源： 题型：
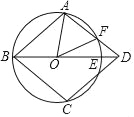
【题目】如图，在⊙O上依次有A、B、C三点，BO的延长线交⊙O于E，
，过点C作CD∥AB交BE的延长线于D，AD交⊙O于点F．
（1）求证：四边形ABCD是菱形；
（2）连接OA、OF，若∠AOF＝3∠FOE且AF＝3，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若干个相同的正方体组成一个几何体，从不同方向看可以得到如图所示的形状，则这个几何体最多可由多少个这样的正方体组成？（ ）
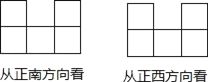
A. 12个 B. 13个 C. 14个 D. 18个
查看答案和解析>>
科目：初中数学 来源： 题型：
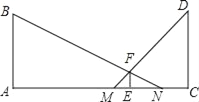
【题目】如图所示，晚上小亮走在大街上，他发现当他站在大街上高度相等的两盏路灯AB和CD之间时，自己右边的影子NE的长为3m，左边的影子ME的长为1.5m，又知小亮的身高EF为1.80m，两盏路灯AC之间的距离为12m，点A、M、E、N、C在同一条直线上，问：路灯的高为多少米？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com