
【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知:⊙O.

求作:⊙O的内接等腰直角三角形.
作法:如图,
①作直径AB;

②分别以点A,B为圆心,以大于![]() 的同样长为半径作弧,两弧交于M,N两点;
的同样长为半径作弧,两弧交于M,N两点;
③作直线MN交⊙O于点C,D;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB是直径, C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 、
、![]() 上分别找点
上分别找点![]() 、
、![]() ,使
,使![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转,
顺时针方向旋转,![]() 的中点
的中点![]() 恰好落在
恰好落在![]() 的中点,延长
的中点,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
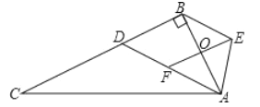
(1)四边形![]() 是什么特殊四边形?说明理由.
是什么特殊四边形?说明理由.
(2)是否存在![]() 中,使得图中四边形
中,使得图中四边形![]() 为菱形?若不存在,说明理由;若存在,求出此时
为菱形?若不存在,说明理由;若存在,求出此时![]() 的面积与
的面积与![]() 面积的倍数关系.
面积的倍数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
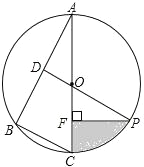
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
(1)若矩形养鸡场的面积为92平方米,求所用的墙长AD.(结果精确到0.1米)(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.24)
=2.24)
(2)求此矩形养鸡场的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
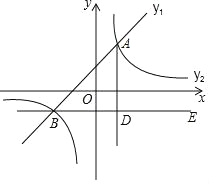
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点E为线段AB上一动点(不与点A,B重合),连接CE,将∠ACE的两边CE,CA分别绕点C顺时针旋转90°,得到射线CE,,CA,,过点A作AB的垂线AD,分别交射线CE,,CA,于点F,G.
(1)依题意补全图形;
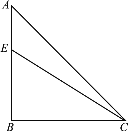
(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示);
(3)用等式表示线段AE,AF与BC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数的对称轴是x=1,图象最低点P的纵坐标是﹣8,图象过(﹣2,10)且与x轴交于A,B与y轴交于C.求:
(1)这个二次函数的解析式;
(2)△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
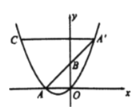
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() .点
.点![]() 是
是![]() 轴正半轴上一点,点
轴正半轴上一点,点![]() 关于点
关于点![]() 的对称点
的对称点![]() 恰好落在抛物线上.过点
恰好落在抛物线上.过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .若点
.若点![]() 的横坐标为1,则
的横坐标为1,则![]() 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校食堂的中餐与晚餐的资费标准如下:
种类 | 单价 |
米饭 | 0.5元/份 |
A类套餐菜 | 3.5元/份 |
B类套餐菜 | 2.5元/份 |
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com