
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 、
、![]() 上分别找点
上分别找点![]() 、
、![]() ,使
,使![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转,
顺时针方向旋转,![]() 的中点
的中点![]() 恰好落在
恰好落在![]() 的中点,延长
的中点,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
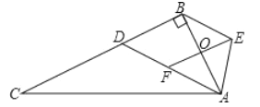
(1)四边形![]() 是什么特殊四边形?说明理由.
是什么特殊四边形?说明理由.
(2)是否存在![]() 中,使得图中四边形
中,使得图中四边形![]() 为菱形?若不存在,说明理由;若存在,求出此时
为菱形?若不存在,说明理由;若存在,求出此时![]() 的面积与
的面积与![]() 面积的倍数关系.
面积的倍数关系.
【答案】(1)四边形![]() 是平行四边形,理由见解析;(2)存在,
是平行四边形,理由见解析;(2)存在,![]() ,理由见解析.
,理由见解析.
【解析】
(1)由于AE=AF,且O是EF中点,根据等腰三角形三线合一的性质知:AO⊥EF,即FO∥BD,从而证得OF是△ABD的中位线,由此可得BD=2OF=EF,那么BD、EF平行且相等,根据一组对边平行且相等的四边形是平行四边形即可判断出四边形BDFE的形状.
(2)当四边形BDFE是菱形时,BD=FD,即AF=2BD,由此可得∠FAO=30°,∠BAC=∠EAF=60°;易证得△FOA∽△ABC,首先求出FO、OA即FO、AB的比例关系,即可得到△AFO、△ABC的面积比,进而可得到△AEF、△ABC的面积比.
解:(1)四边形![]() 是平行四边形;
是平行四边形;
理由:∵![]() ,且
,且![]() 是
是![]() 中点,
中点,
∴![]() ,即
,即![]() ;
;
∵![]() 是
是![]() 中点,
中点,
∴![]() 是
是![]() 的中位线,即
的中位线,即![]() ,
,
∴![]() 、
、![]() 平行且相等,
平行且相等,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)若四边形![]() 是菱形,则
是菱形,则![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,即
,即![]() ;
;
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y1=﹣x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(﹣1,5),点A与y1的顶点B的距离是4.
(1)求y1的解析式;
(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小;
(3)画出以AB为直径的⊙O,交AD于点E,连接BE与AP交于点F,若tan∠BPC=![]() ,求tan∠AFE的值.
,求tan∠AFE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:
①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
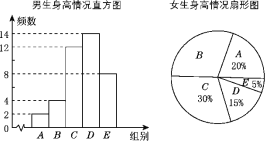
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在________组(填组别序号),女生身高在B组的人数有________人;
(2)在样本中,身高在150≤x<155之间的人数共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人、女生480人,请估计身高在155≤x<165之间的学生有多少人
查看答案和解析>>
科目:初中数学 来源: 题型:
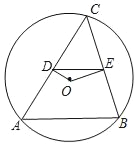
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为x=1,与y轴的交点B在(0,2)和(0,3)之间(包含这两个点)运动.有如下四个结论:①抛物线与x轴的另一个交点是(3,0);②点C(x1,y1),D(x2,y2)在抛物线上,且满足x1<x2<1,则y1>y2;③常数项c的取值范围是2≤c≤3;④系数a的取值范围是﹣1≤a≤﹣![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知:⊙O.

求作:⊙O的内接等腰直角三角形.
作法:如图,
①作直径AB;

②分别以点A,B为圆心,以大于![]() 的同样长为半径作弧,两弧交于M,N两点;
的同样长为半径作弧,两弧交于M,N两点;
③作直线MN交⊙O于点C,D;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB是直径, C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com