
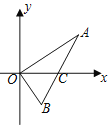
【题目】如图,在直角坐标平面xOy中,点A坐标为![]() ,
,![]() ,
,![]() ,AB与x轴交于点C,那么AC:BC的值为______.
,AB与x轴交于点C,那么AC:BC的值为______.
【答案】![]()
【解析】
过点A作AD⊥y轴,垂足为D,作BE⊥y轴,垂足为E.先证△ADO∽△OEB,再根据∠OAB=30°求出三角形的相似比,得到OD:OE=2∶![]() ,根据平行线分线段成比例得到AC:BC=OD:OE=2∶
,根据平行线分线段成比例得到AC:BC=OD:OE=2∶![]() =
=![]()
解:
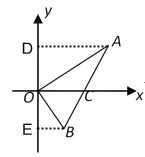
如图所示:过点A作AD⊥y轴,垂足为D,作BE⊥y轴,垂足为E.
∵∠OAB=30°,∠ADE=90°,∠DEB=90°
∴∠DOA+∠BOE=90°,∠OBE+∠BOE=90°
∴∠DOA=∠OBE
∴△ADO∽△OEB
∵∠OAB=30°,∠AOB=90°,
∴OA∶OB=![]()
∵点A坐标为(3,2)
∴AD=3,OD=2
∵△ADO∽△OEB
∴![]()
∴OE![]()
∵OC∥AD∥BE
根据平行线分线段成比例得:
AC:BC=OD:OE=2∶![]() =
=![]()
故答案为![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
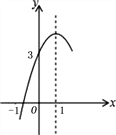
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① 4ac<b2;② 方程ax2+bx+c=0的两个根是![]() ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
其中结论正确有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
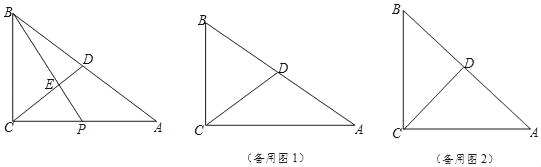
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 、
、![]() 上分别找点
上分别找点![]() 、
、![]() ,使
,使![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转,
顺时针方向旋转,![]() 的中点
的中点![]() 恰好落在
恰好落在![]() 的中点,延长
的中点,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
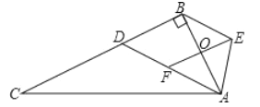
(1)四边形![]() 是什么特殊四边形?说明理由.
是什么特殊四边形?说明理由.
(2)是否存在![]() 中,使得图中四边形
中,使得图中四边形![]() 为菱形?若不存在,说明理由;若存在,求出此时
为菱形?若不存在,说明理由;若存在,求出此时![]() 的面积与
的面积与![]() 面积的倍数关系.
面积的倍数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy(如图)中,抛物线y=ax2+bx+2经过点A(4,0)、B(2,2),与y轴的交点为C.
(1)试求这个抛物线的表达式;
(2)如果这个抛物线的顶点为M,求△AMC的面积;
(3)如果这个抛物线的对称轴与直线BC交于点D,点E在线段AB上,且∠DOE=45°,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
(1)若矩形养鸡场的面积为92平方米,求所用的墙长AD.(结果精确到0.1米)(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.24)
=2.24)
(2)求此矩形养鸡场的最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com