
【题目】在平面直角坐标系xOy(如图)中,抛物线y=ax2+bx+2经过点A(4,0)、B(2,2),与y轴的交点为C.
(1)试求这个抛物线的表达式;
(2)如果这个抛物线的顶点为M,求△AMC的面积;
(3)如果这个抛物线的对称轴与直线BC交于点D,点E在线段AB上,且∠DOE=45°,求点E的坐标.
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)点E的坐标为(3,1).
;(3)点E的坐标为(3,1).
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出抛物线的表达式;
(2)利用配方法可求出点M的坐标,利用二次函数图象上点的坐标特征可求出点C的坐标,过点M作MH⊥y轴,垂足为点H,利用分割图形求面积法可得出△AMC的面积;
(3)连接OB,过点B作BG⊥x轴,垂足为点G,则△BGA,△OCB是等腰直角三角形,进而可得出∠BAO=∠DBO,由∠DOB+∠BOE=45°,∠BOE+∠EOA=45°可得出∠EOA=∠DOB,进而可证出△AOE∽△BOD,利用相似三角形的性质结合抛物线的对称轴为直线x=1可求出AE的长,过点E作EF⊥x轴,垂足为点F,则△AEF为等腰直角三角形,根据等腰直角三角形的性质可得出AF、EF的长,进而可得出点E的坐标.
解:(1)将A(4,0),B(2,2)代入y=ax2+bx+2,得:![]() ,
,
解得: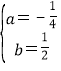 ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴顶点M的坐标为(1,![]() ).
).
当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
∴点C的坐标为(0,2).
过点M作MH⊥y轴,垂足为点H,如图1所示.
∴S△AMC=S梯形AOHM﹣S△AOC﹣S△CHM,
=![]() (HM+AO)OH﹣
(HM+AO)OH﹣![]() AOOC﹣
AOOC﹣![]() CHMH,
CHMH,
=![]() ×(1+4)×
×(1+4)×![]() ﹣
﹣![]() ×4×2﹣
×4×2﹣![]() ×(
×(![]() ﹣2)×1,
﹣2)×1,
=![]() .
.
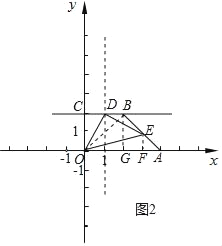
(3)连接OB,过点B作BG⊥x轴,垂足为点G,如图2所示.
∵点B的坐标为(2,2),点A的坐标为(4,0),
∴BG=2,GA=2,
∴△BGA是等腰直角三角形,
∴∠BAO=45°.
同理,可得:∠BOA=45°.
∵点C的坐标为(2,0),
∴BC=2,OC=2,
∴△OCB是等腰直角三角形,
∴∠DBO=45°,BO=2![]() ,
,
∴∠BAO=∠DBO.
∵∠DOE=45°,
∴∠DOB+∠BOE=45°.
∵∠BOE+∠EOA=45°,
∴∠EOA=∠DOB,
∴△AOE∽△BOD,
∴![]() .
.
∵抛物线y=﹣![]() x2+
x2+![]() x+2的对称轴是直线x=1,
x+2的对称轴是直线x=1,
∴点D的坐标为(1,2),
∴BD=1,
∴![]() ,
,
∴AE=![]() ,
,
过点E作EF⊥x轴,垂足为点F,则△AEF为等腰直角三角形,
∴EF=AF=1,
∴点E的坐标为(3,1).


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
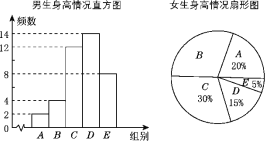
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在________组(填组别序号),女生身高在B组的人数有________人;
(2)在样本中,身高在150≤x<155之间的人数共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人、女生480人,请估计身高在155≤x<165之间的学生有多少人
查看答案和解析>>
科目:初中数学 来源: 题型:
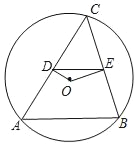
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
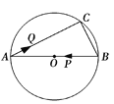
【题目】如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为x=1,与y轴的交点B在(0,2)和(0,3)之间(包含这两个点)运动.有如下四个结论:①抛物线与x轴的另一个交点是(3,0);②点C(x1,y1),D(x2,y2)在抛物线上,且满足x1<x2<1,则y1>y2;③常数项c的取值范围是2≤c≤3;④系数a的取值范围是﹣1≤a≤﹣![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
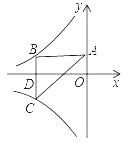
【题目】如图所示双曲线y=![]() 与y=﹣
与y=﹣![]() 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣
分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,![]() );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ∥
∥![]() ,⊙O与
,⊙O与![]() 和
和![]() 分别相切于点A和点B.点M和点N分别是
分别相切于点A和点B.点M和点N分别是![]() 和
和![]() 上的动点,MN沿
上的动点,MN沿![]() 和
和![]() 平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
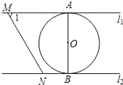
A. ![]() B. l1和l2的距离为2
B. l1和l2的距离为2
C. 若∠MON=90°,则MN与⊙O相切 D. 若MN与⊙O相切,则![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com