
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表给出了以下结论:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y=ax2+bx+c有最小值,最小值为﹣3;②当﹣![]() <x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
<x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】
利用x=﹣1和x=3时函数值都为0可判断抛物线与x轴有两个交点坐标为(﹣1,0),(3,0),则可对③进行判断;利用表中数据得到当﹣1<x<3时,y<0,则可对②进行判断;利用对称性得到抛物线的对称轴为直线x=1,则可对①进行判断;根据二次函数的性质可对④进行判断.
∵x=﹣1和x=3时,y=0,
∴抛物线与x轴有两个交点坐标为(﹣1,0),(3,0),所以③正确;
∴当﹣1<x<3时,y<0,所以②错误;
∵点(﹣1,0)与(3,0)为抛物线上的对称点,
∴抛物线的对称轴为直线x=1,
∴当x=1时,二次函数有最小值﹣4,所以①错误;
∵抛物线开口向上,
∴当x<1时,y随x的增大而减小,所以④正确.
故选C.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】为了提倡“保护自然资源,节约自然资源”,某部门对某县一次性筷子的用量进行了调查.2015年从该县600家高、中、低档饭店中抽取了10家进行调查,得知这些饭店每天消耗的一次性筷子的盒数分别为:0.6,3.7,2.2,1.5,2.8,1.7,1.2,2.1,3.2,1.0.
(1)估计该县2015年各饭店共消耗多少盒一次性筷子?(一年按350个营业日计算)
(2)在(1)的条件下,若生产一套学生课桌椅需木材0.07 m3,则该县2015年各饭店使用一次性筷子所消耗的木材可以生产多少套学生课桌椅?(计算中需用到的有关数据为:每盒筷子100双,每双筷子的质量为5 g,所用木材的密度为0.5×103 kg/m3)
(3)通过以上计算,你对保护自然资源有什么看法?请提出两条合理的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
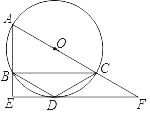
【题目】如图,已知AC是⊙O的直径,B为⊙O上一点,D为![]() 的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
(Ⅰ)求证:EF为⊙O的切线;
(Ⅱ)若AB=2,∠BDC=2∠A,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
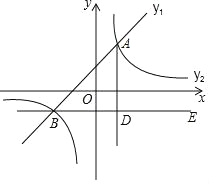
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
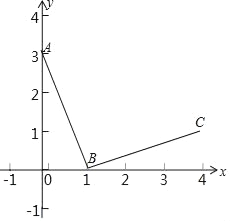
【题目】如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y=![]() 的图象G经过点C.
的图象G经过点C.
(1)请直接写出点C的坐标及k的值;
(2)若点P在图象G上,且∠POB=∠BAO,求点P的坐标;
(3)在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数的对称轴是x=1,图象最低点P的纵坐标是﹣8,图象过(﹣2,10)且与x轴交于A,B与y轴交于C.求:
(1)这个二次函数的解析式;
(2)△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
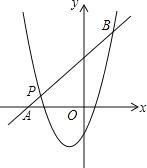
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
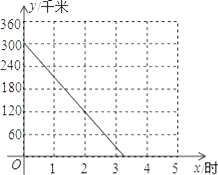
【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com