
【题目】如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM. 
(1)求线段PM的长;
(2)在第一象限内找一点N,使四边形OPNM是平行四边形,画出图形并求出点N的坐标(保留作图痕迹)
【答案】
(1)解:过P点作PA⊥x轴于点A,
在Rt△PAM中,PA=12,AM=14﹣9=5,
则PM= ![]() =13
=13
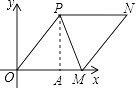
(2)解:如图所示:点N的坐标为(9+14=23,12),即(23,12)
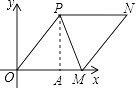
【解析】(1)过P点作PA⊥x轴于点A,在Rt△PAM中,根据勾股定理可求PM;(2)运用平行四边形性质,可知PN∥OM,所以点N的纵坐标是12,再根据OM间的距离即可推导出点N的横坐标,从而求解.
【考点精析】认真审题,首先需要了解平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形).


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣6x﹣5=0,此方程可化为( )
A. (x﹣3)2=4 B. (x﹣3)2=14 C. (x﹣9)2=4 D. (x﹣9)2=14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). 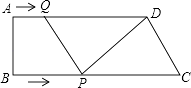
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C、D、Q、P为顶点的梯形面积等于60cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com