
【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
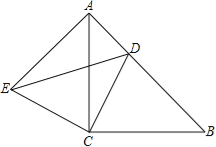
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
【答案】(1)证明见解析;(2)13.
【解析】
试题(1)根据等腰直角三角形得出AC=BC,CE=CD,∠ACB=∠ECD=90°,求出∠BCD=∠ACE,根据SAS推出△BCD≌△ACE即可.
(2)求出AD=5,根据全等得出AE=BD=12,在Rt△AED中,由勾股定理求出DE即可.
试题解析:(1)∵△ACB与△ECD都是等腰直角三角形,∴AC=BC,CE=CD,
∵∠ACB=∠ECD=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,∴∠BCD=∠ACE,
在△BCD和△ACE中,∵BC=AC,∠BCD=∠ACE,CD=CE,∴△BCD≌△ACE(SAS).
(2)由(1)知△BCD≌△ACE,则∠DBC=∠EAC,
∵∠CAD+∠DBC=90°,∴∠EAC+∠CAD=90°,即∠EAD=90°
∵AB=17,BD=12,∴AD=17﹣12=5,
∵△BCD≌△ACE,∴AE=BD=12,
在Rt△AED中,由勾股定理得:DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读理解
如图(1),在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2 , 并以线段A1B2为边在线段A1A2的上方作以正多边形A1B2B3…Bn , 把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形,点A3称为准位似中心.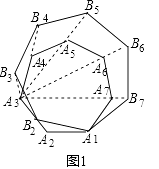
特例论证
(1)如图(2)已知正三角形A1A2A3的准位似图形为正三角形A1B2B3 , 试证明:随着点B2的运动,∠B3A3A1的大小始终不变.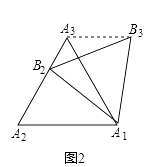
(2)如图(3)已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4 , 随着点B2的运动,∠B3A3A4的大小始终不变?若不变,请求出∠B3A3A4的大小;若改变,请说明理由.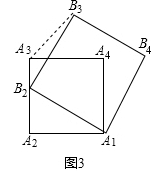
(3)在图(1)的情况下:
①试猜想∠B3A3A4的大小是否会发生改变?若不改变,请用含n的代数式表示出∠B3A3A4的大小(直接写出结果);若改变,请说明理由.
①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1= ![]() (用含n的代数式表示)
(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减轻学生课业负担,提高课堂效果,我县教体局积极推进 “高效课堂”建设.
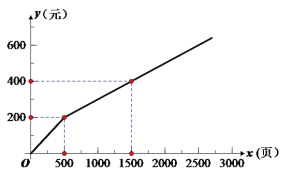
某学校的《课堂检测》印刷任务原来由甲复印店承接,其每月收费y(元)与复印页数x(页)的函数关系如图所示:
⑴从图象中可看出:每月复印超过500页部分每页收费 元;
⑵现在乙复印店表示:若学校先按每月付给200元的月承包费,则可按每页0.15元收费.乙复印店每月收费y(元)与复印页数x(页)的函数关系为 ;
⑶在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答每月复印在3000页左右应选择哪个复印店?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD. 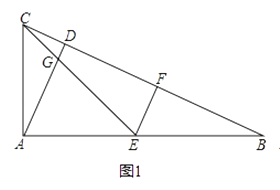
(2)如图2,AC:AB=1: ![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值. 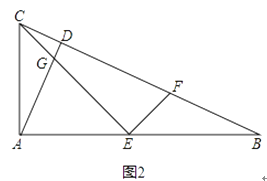
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数 ![]() 的四个命题:①当
的四个命题:①当 ![]() 时,
时, ![]() 有最小值10;②
有最小值10;② ![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于 ![]() 时的函数值;③若
时的函数值;③若 ![]() ,且
,且 ![]() 是整数,当
是整数,当 ![]() 时,
时, ![]() 的整数值有
的整数值有 ![]() 个;④若函数图象过点
个;④若函数图象过点 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,则
,则 ![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.①
B.②
C.③
D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
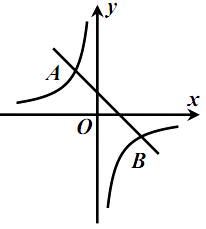
【题目】如图,一次函数 ![]() (
( ![]() )与反比例函数
)与反比例函数 ![]() (
( ![]() )的图象交于点
)的图象交于点 ![]() ,
, ![]() .
.
(1)求这两个函数的表达式;
(2)在 ![]() 轴上是否存在点
轴上是否存在点 ![]()
![]() ,使
,使 ![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知在△ABC中,∠C=90°,AC=5,AB=13.点D在边AC上,且点D到边AB和边BC的距离相等.
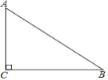
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求△ABD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com