
【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
【答案】C
【解析】
作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.利用待定系数法求出直线AB′的解析式,然后求出其与x轴交点的坐标,即M点的坐标.
如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
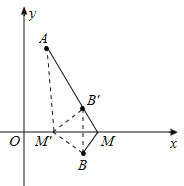
不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B′.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边).
∴M′A-M′B<AM-BM,即此时AM-BM最大.
∵B′是B(3,-1)关于x轴的对称点,
∴B′(3,1).
设直线AB′解析式为y=kx+b,把A(1,3)和B′(3,1)代入得:
![]() ,
,
解之得
![]() ,
,
∴直线AB′解析式为y=-x+4.
令y=0,解得x=4,
∴M点坐标为(4,0).
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )

A.y=﹣x B.y=﹣![]() x C.y=﹣
x C.y=﹣![]() x D.y=﹣
x D.y=﹣![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
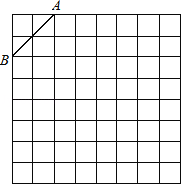
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表) 甲超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 5 | 10 | 5 |
乙超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 10 | 5 | 10 |
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
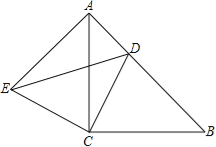
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.

古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c,设p=![]() ,则三角形的面积S=
,则三角形的面积S=![]() .
.
我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c,则三角形的面积S=![]() .
.
(1)若一个三角形的三边长分别是5,6,7,求这个三角形的面积.
(2)若一个三角形的三边长分别是![]() ,求这个三角形的面积.
,求这个三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道 ![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 ![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 ![]() ﹣1来表示
﹣1来表示 ![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为 ![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<(
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<( ![]() )2<32 , 即2<
)2<32 , 即2< ![]() <3,∴
<3,∴ ![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( ![]() ﹣2). 请解答:
﹣2). 请解答:
(1)![]() 的整数部分是 , 小数部分是
的整数部分是 , 小数部分是
(2)如果 ![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣ ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com