
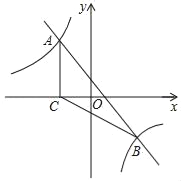
【题目】如图,直线y=﹣x+1与反比例函数y=![]() 的图象相交于点A、B,过点A作AC⊥x轴,垂足为点C(﹣2,0),连接AC、BC.
的图象相交于点A、B,过点A作AC⊥x轴,垂足为点C(﹣2,0),连接AC、BC.
(1)求反比例函数的解析式;
(2)求S△ABC;
(3)利用函数图象直接写出关于x的不等式﹣x+1<![]() 的解集.
的解集.
【答案】解:(1)y=﹣![]() ;(2)7.5;(3)﹣2<x<0或x>3.
;(2)7.5;(3)﹣2<x<0或x>3.
【解析】
(1)根据C点的横坐标和点A在直线上,求出点A的坐标,代入反比例函数的解析式即可。
(2)根据一次函数和反比例函数的解析式求出B点坐标,求出直线AB与x轴的交点D的坐标,再根据三角形ABC的面积=根据三角形ADC的面积+根据三角形DBC的面积即可
(3)结合A、B两点坐标,观察图象即可得出。
(1)∵AC⊥x轴,点C(﹣2,0),∴A点横坐标为-2,
当x=-2时,y=2+1=3,∴A(-2,3)
∵A(-2,3)反比例函数y=![]() 的图象,∴k=-6,
的图象,∴k=-6,
∴y=﹣![]() ;
;
(2)解方程组: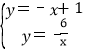 ,
,
解得:![]() 或
或![]()
∴B(3,-2)
设直线AB交x轴于点D,对于y=-x+1,
当y=0时,x=1
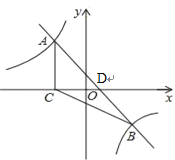
∴D(1,0)∴CD=3
∴△ABC的面积=△ADC的面积+△DBC的面积=![]() ×3×3+
×3×3+![]() ×3×2=7.5.
×3×2=7.5.
(3)由图得,当-2<x<0或x>3时,反比例函数值大于一次函数值;
∴关于x的不等式﹣x+1<![]() 的解集为:-2<x<0或x>3
的解集为:-2<x<0或x>3


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
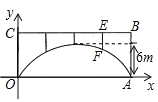
【题目】如图,一座拱桥的轮廓是抛物线型,拱高6![]() ,在长度为8
,在长度为8![]() 的两支柱
的两支柱![]() 和
和![]() 之间,还安装着三根支柱,相邻两支柱间的距离为5
之间,还安装着三根支柱,相邻两支柱间的距离为5![]() .
.
(1)建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;
(2)求支柱![]() 的长度.
的长度.
(3)拱桥下面拟铺设行车道,要保证高3![]() 的汽车能够通过(车顶与拱桥的距离不小于0.3
的汽车能够通过(车顶与拱桥的距离不小于0.3![]() ),行车道最宽可以铺设多少米?
),行车道最宽可以铺设多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解九年级学生寒假的阅读情况,随机抽取了该年级的部分学生进行调查,统计了他们每人的阅读本数,设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x,y的值;
(2)求扇形统计图中“优秀”类所在扇形的圆心角的度数;
(3)如果随机去掉一个数据,求众数发生变化的概率,并指出众数变化时,去掉的是哪个数据.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/21/2208296361205760/2209339150721024/STEM/fd85c35161634f71b20809e4321f104b.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求此反比例函数的解析式;
(2)问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?
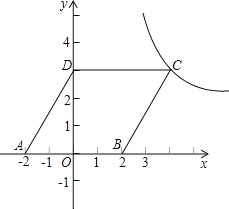
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径是2,弦AB=![]() ,点C为是优弧AB上一个动点,BD⊥BC交直线AC于点D,则△ABD的面积的最大值为___________ .
,点C为是优弧AB上一个动点,BD⊥BC交直线AC于点D,则△ABD的面积的最大值为___________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
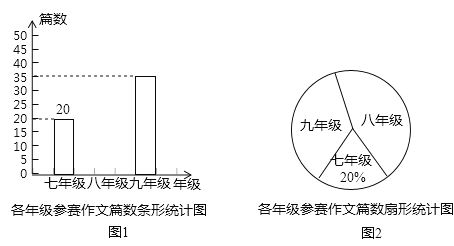
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com