
【题目】如图,⊙O的半径是2,弦AB=![]() ,点C为是优弧AB上一个动点,BD⊥BC交直线AC于点D,则△ABD的面积的最大值为___________ .
,点C为是优弧AB上一个动点,BD⊥BC交直线AC于点D,则△ABD的面积的最大值为___________ .

【答案】3![]()
【解析】
连结OA,如图,∠AOB=120°,根据圆周角定理得∠ACB=![]() ∠AOB=60°,由于BC⊥BD,所以∠D=30°,因为AB=
∠AOB=60°,由于BC⊥BD,所以∠D=30°,因为AB=![]() ,则要使△ABD的最大面积,点D到AB的距离要最大;当点D在⊙M上的优弧AB的中点时,点D到AB的距离最大,从而得到△ABD的最大面积.
,则要使△ABD的最大面积,点D到AB的距离要最大;当点D在⊙M上的优弧AB的中点时,点D到AB的距离最大,从而得到△ABD的最大面积.
解:连结OA,过点O作OE垂直AB,交AB与点E
已知⊙O的半径是2,弦AB=![]() ,BE⊥BC,根据垂径定理和勾股定理可得
,BE⊥BC,根据垂径定理和勾股定理可得
OE=1,AE=![]() ,sin∠OAE=
,sin∠OAE=![]()
∴∠OAE=∠OBE=30°
![]()
![]() (同弧所对的圆周角是圆心角的一半)
(同弧所对的圆周角是圆心角的一半)
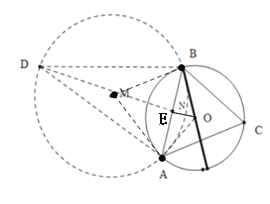
∠ADB =30°,点D在以AB为弦的⊙M上运动,
∠BMA=60°,
AB=MB=DM=MA=![]() ,
,
当点D在优弧AB的中点时,点D到AB的距离最大,从而得到△ABD的最大面积.
过点D作DN⊥AB于点N![]()
![]()
![]()
![]()
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 中,延长
中,延长![]() 到点
到点![]() ,点
,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,
,![]() 分别交
分别交![]() 、
、![]() 的平分线于
的平分线于![]() ,
,![]() 两点,连接
两点,连接![]() 、
、![]() .在下列结论中.①
.在下列结论中.①![]() ;②
;②![]() ;③若
;③若![]() ,
,![]() ,则
,则![]() 的长为6;④当
的长为6;④当![]() 时,四边形
时,四边形![]() 是矩形.其中正确的是( )
是矩形.其中正确的是( )

A. ①④B. ①②C. ①②③D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
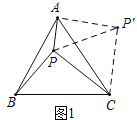
【题目】(1)阅读理解
利用旋转变换解决数学问题是一种常用的方法.如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.
为利用已知条件,不妨把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,则
,则![]() 的长为_______;在
的长为_______;在![]() 中,易证
中,易证![]() ,且
,且![]() 的度数为________,综上可得
的度数为________,综上可得![]() 的度数为_______;
的度数为_______;
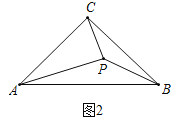
(2)类比迁移
如图,点![]() 是等腰
是等腰![]() 内的一点,
内的一点,![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数;
的度数;
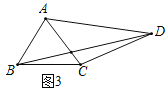
(3)拓展应用
如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一棵古树![]() 和教学楼
和教学楼![]() 的高,先在
的高,先在![]() 处用高1.5米的测角仪测得古树顶端
处用高1.5米的测角仪测得古树顶端![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端
,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走9米到达
上,再向前走9米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
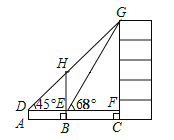
(1)计算古树![]() 的高;
的高;
(2)计算教学楼![]() 的高.(结果精确到0.1米,参考数据:
的高.(结果精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+1与反比例函数y=![]() 的图象相交于点A、B,过点A作AC⊥x轴,垂足为点C(﹣2,0),连接AC、BC.
的图象相交于点A、B,过点A作AC⊥x轴,垂足为点C(﹣2,0),连接AC、BC.
(1)求反比例函数的解析式;
(2)求S△ABC;
(3)利用函数图象直接写出关于x的不等式﹣x+1<![]() 的解集.
的解集.
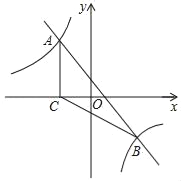
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 ![]() 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
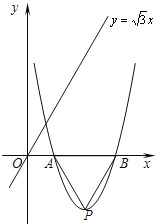
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与x轴分别交于点A.B,与y轴交于点C,A点坐标为(-1,0),B点坐标为(3,0),顶点为D.
(1)求抛物线解析式;
(2)若点M在抛物线的对称轴上,求△ACM周长的最小值;
(3)以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标.
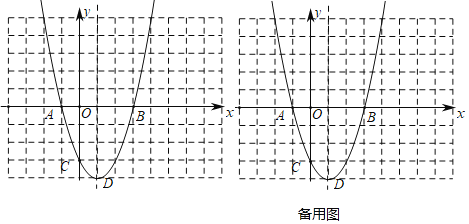
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是
A. Rt△ABC中,AB=3,BC=4,则AC=5;
B. 极差能反映一组数据的变化范围;
C. 经过点A(2,3)的双曲线一定经过点B(-3,-2);
D. 连接菱形各边中点所得的四边形是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com