
【题目】已知抛物线![]() 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 ![]() 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
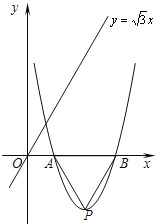
【答案】(1)![]() ,P的坐标为(4,
,P的坐标为(4,![]() ),B的坐标是(6,0)(2)D点的坐标为(2,
),B的坐标是(6,0)(2)D点的坐标为(2, ![]() )(3)存在,证明见解析
)(3)存在,证明见解析
【解析】解:(1)∵抛物线![]() 经过A(2,0),
经过A(2,0),
∴![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为![]() 。
。
∵![]() ,
,
∴顶点P的坐标为(4,![]() )。
)。
令y=0,得![]() ,解得
,解得![]() 。
。
∴点B的坐标是(6,0)。
(2)在直线 ![]() 上存在点D,使四边形OPBD为平行四边形。理由如下:
上存在点D,使四边形OPBD为平行四边形。理由如下:
设直线PB的解析式为![]() ,把B(6,0),P(4,
,把B(6,0),P(4, ![]() )分别代入,得
)分别代入,得
![]() , 解得
, 解得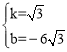 。
。
∴直线PB的解析式为![]() 。
。
又∵直线OD的解析式为![]()
∴直线PB∥OD。
设直线OP的解析式为![]() ,把P(4,
,把P(4, ![]() )代入,得
)代入,得
![]() ,解得
,解得![]() 。
。
如果OP∥BD,那么四边形OPBD为平行四边形。
设直线BD的解析式为![]() ,将B(6,0)代入,得
,将B(6,0)代入,得
![]() ,解得
,解得![]() 。
。
∴直线BD的解析式为![]() 。
。
联立方程组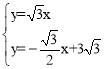 ,解得
,解得![]() 。
。
∴D点的坐标为(2, ![]() )。
)。
(3)符合条件的点M存在。验证如下:
过点P作x轴的垂线,垂足为为C,
则PC=![]() ,AC=2,
,AC=2,
由勾股定理,可得AP=4,PB=4。
又∵AB=4,∴△APB是等边三角形。
作∠PAB的平分线交抛物线于M点,连接PM,BM。
∵AM=AM,∠PAM=∠BAM,AB=AP,∴△AMP≌△AMB.(SAS)。
因此即存在这样的点M,使△AMP≌△AMB.。
(1)由抛物线![]() 经过A(2,0),代入即可求出b的值;从而得出抛物线的解析式,化为顶点式即可求出顶点P的坐标;令y=0,即可求出点B的坐标。
经过A(2,0),代入即可求出b的值;从而得出抛物线的解析式,化为顶点式即可求出顶点P的坐标;令y=0,即可求出点B的坐标。
(2)用待定系数法,求出直线PB、BD的解析式,联立![]() 和
和![]() ,解之即得点D的坐标。
,解之即得点D的坐标。
(3)由勾股定理求出AP、BP和AB的长,证出△APB是等边三角形,即可作BP的中垂线AM交BP于点M,点M即为所求。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)

(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+m的图象与x轴y轴分别交于点A,B,与正比例函数y=![]() x的图象交于点P(2,n)
x的图象交于点P(2,n)
(1)求点A的坐标;
(2)求△POB的面积.
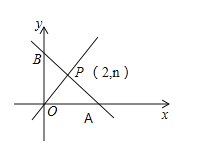
查看答案和解析>>
科目:初中数学 来源: 题型:
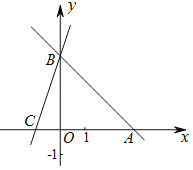
【题目】如图,直线y=﹣x+b分别与x轴、y轴交于A,B两点,点A的坐标为(3,0),过点B的另一条直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求点B的坐标及直线BC对应的函数表达式;
(2)在线段OB上存在点P,使得点P到点B,C的距离相等,试求出点P的坐标;
(3)如果在x轴上方存在点D,使得以点A,B,D为顶点的三角形与△ABC全等,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣(3m+1)x+2m2+m(m>0),与y轴交于点C,与x轴交于点A(x1,0),B(x2,0),且x1<x2.
(1)求2x1﹣x2+3的值;
(2)当m=2x1﹣x2+3时,将此抛物线沿对称轴向上平移n个单位,使平移后得到的抛物线顶点落在△ABC的内部(不包括△ABC的边),求n的取值范围(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),在
重合),在![]() 同侧分别作等边
同侧分别作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .下列五个结论:①
.下列五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④DE=DP;⑤
;④DE=DP;⑤![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com