
分析 用十字相乘法解二元二次方程,用含y的代数式表示出x,分别代入$\frac{x}{y}$和$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+xy}$约分后的分式,计算出它们的值.
解答 解:因为x2+5xy+6y2=0,
所以(x+2y)(x+3y)=0
所以x=-2y或-3y
把x=-2y或-3y代入$\frac{x}{y}$,
原式=$\frac{-2y}{y}=-2$,或$\frac{-3y}{y}=-3$;
由于$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+xy}$=$\frac{x-y}{x}$,
把x=-2y或-3y代入$\frac{x-y}{x}$,
原式=$\frac{-2y-y}{-2y}$=$\frac{3}{2}$或=$\frac{-3y-y}{-3y}$=$\frac{4}{3}$.
所以代数式$\frac{x}{y}$和$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+xy}$的值分别是-2,-3和$\frac{3}{2}$,$\frac{4}{3}$.
点评 本题考查了二元二次方程的解法、分式的化简求值.用含y的代数式表示x是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)
如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
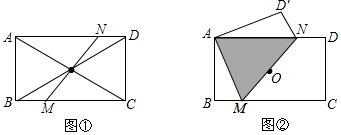
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sin60°-sin30°=sin30° | B. | sin245°+cos245°=1 | ||
| C. | (tan60°)2=3 | D. | tan30°=$\frac{sin30°}{cos30°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
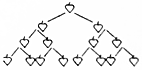 如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果,第五行有16个苹果…,猜猜第2017行有22016个苹果.
如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果,第五行有16个苹果…,猜猜第2017行有22016个苹果.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com