
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 将对角线
将对角线![]() 三等分,且
三等分,且![]() ,连接
,连接![]() .
.
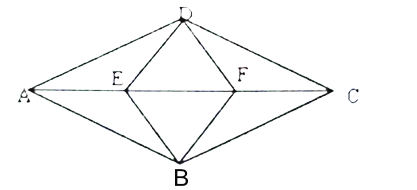
(1)求证:四边形![]() 为菱形
为菱形
(2)求菱形![]() 的面积;
的面积;
(3)若![]() 是菱形
是菱形![]() 的边上的点,则满足
的边上的点,则满足![]() 的点
的点![]() 的个数是______个.
的个数是______个.
【答案】(1)见解析;(2)![]() ;(3)8
;(3)8
【解析】
(1)根据题意证明△AED≌△AEB≌△CFD≌△CFB,得到四边相等即可证明是菱形;
(2)求出菱形的对角线的长,利用菱形的面积等于对角线乘积的一半解决问题即可.
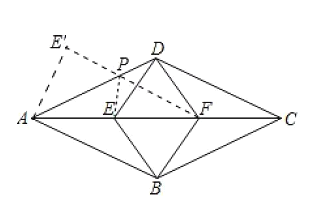
(3)不妨假设点P在线段AD上,作点E关于AD的对称点E′,连接FE′交AD于点P,此时PE+PF的值最小.求出PE+PF的最值,判断出在线段AD上存在两个点P满足条件,由此即可判断.
(1)∵四边形ABCD是菱形,
∴AD≡AB=CD=CB,∠DAE=∠BAE=∠DCF=∠BCF,
∴△AED≌△AEB≌△CFD≌△CFB(SAS)
∴DE=BE=DF=BF,
∴四边形DEBF为菱形.
(2)连接DB,交AC于O,

∵四边形ABCD是菱形,
∴DB⊥AC,![]() ,
,
又∵AE=EF=FC=2,
∴AO=3,AD=2DO,
∴![]() ,∴
,∴![]() ,
,
∴![]()
(3)不妨假设点P在线段AD上,作点E关于AD的对称点E′,连接FE′交AD于点P,此时PE+PF的值最小.
易知PE+PF的最小值=2![]()
当点P由A运动到D时,PE+PF的值由最大值6减小到2![]() 再增加到4,
再增加到4,
∵PE+PE=![]() ,2
,2![]() <
<![]() <4,
<4,
∴线段AD上存在两个点P,满足PE+PF=![]()
∴根据对称性可知:菱形ABCD的边上的存在8个点P满足条件.
故答案为8.


科目:初中数学 来源: 题型:
【题目】在郴州市的日常工作中,洒水车每天都在国庆路上来回洒水.我们约定洒水车在行驶过程中,向北的行程记为正数,向南的行程记为负数.2017年8月20日这一天,某台洒水车市政工程处出发,所走的路程(单位:千米)为:+5,+7.5,-8,-3,+9.5,+2.5,-11,-3.5.问:
(1)这天收工时,这台洒水车离市政工程处多远?它在市政工程处的南边还是北边?
(2)若洒水车每走1千米耗油0.2升,请问这一天这台洒水车在洒水过程中耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
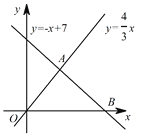
【题目】如图,已知一次函数![]() 与正比例函数
与正比例函数![]() 的图象交于点
的图象交于点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出点![]() 的坐标为 ;点
的坐标为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线l∥y轴.动点
作直线l∥y轴.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长的速度,沿
个单位长的速度,沿![]() 的路线向点
的路线向点![]() 运动;同时直线
运动;同时直线![]() 从点
从点![]() 出发,以相同速度向左平移,在平移过程中,直线
出发,以相同速度向左平移,在平移过程中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 或线段
或线段![]() 于点
于点![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 和直线
和直线![]() 都停止运动.在运动过程中,设动点
都停止运动.在运动过程中,设动点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
![]() 当
当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() ;
;
![]() 是否存在以
是否存在以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?若存在,直接写出
为顶点的三角形是等腰三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
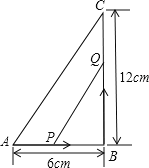
【题目】如图,在![]() 中,
中,![]() ,点P从点A开始,沿AB向点B以
,点P从点A开始,沿AB向点B以![]() 的速度移动,点Q从B点开始沿BC以
的速度移动,点Q从B点开始沿BC以![]() 的速度移动,如果P、Q分别从A、B同时出发:
的速度移动,如果P、Q分别从A、B同时出发:
![]() 几秒后四边形APQC的面积是31平方厘米;
几秒后四边形APQC的面积是31平方厘米;
![]() 若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
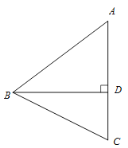
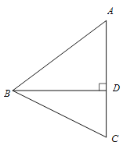
【题目】如图,在△ABC中,AB=AC>BC,BD 是AC边上的高,点C关于直线BD的对称点为点E,连接BE.
(1)①依题意补全图形;
②若∠BAC=![]() ,求∠DBE的大小(用含
,求∠DBE的大小(用含![]() 的式子表示);
的式子表示);
(2)若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“全民阅读”,某校为调查了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成统计图表如下:
学生家庭藏书情况扇形统计图

类别 | 家庭藏书 | 学生人数 |
|
| 16 |
|
|
|
|
| 50 |
|
| 70 |
根据以上信息,解答下列问题:
(1)共抽样调查了______名学生,![]() ______;
______;
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为_______
”对应扇形的圆心角为_______![]() ;
;
(3)若该校有2000名学生,请估计全校学生中家庭藏书超过60本的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com