
����Ŀ����ͼ����֪һ�κ���![]() ������������
������������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ������
������![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
(1)ֱ��д����![]() ������Ϊ ����
������Ϊ ����![]() ������Ϊ ��
������Ϊ ��
(2)����![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��ֱ��l��y�ᣮ����
��ֱ��l��y�ᣮ����![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ�����ٶȣ���
����λ�����ٶȣ���![]() ��·�����
��·�����![]() �˶���ͬʱֱ��
�˶���ͬʱֱ��![]() �ӵ�
�ӵ�![]() ����������ͬ�ٶ�����ƽ�ƣ���ƽ�ƹ����У�ֱ��
����������ͬ�ٶ�����ƽ�ƣ���ƽ�ƹ����У�ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() �����߶�
�����߶�![]() ���߶�
���߶�![]() �ڵ�
�ڵ�![]() ������
������![]() �����
�����![]() ʱ����
ʱ����![]() ��ֱ��
��ֱ��![]() ��ֹͣ�˶������˶������У��趯��
��ֹͣ�˶������˶������У��趯��![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() �룮
�룮
![]() ��
��![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ��
��![]() ��
��![]() Ϊ����������ε����Ϊ
Ϊ����������ε����Ϊ![]() ��
��
![]() �Ƿ������
�Ƿ������![]() ��
��![]() ��
��![]() Ϊ������������ǵ���������?�����ڣ�ֱ��д��
Ϊ������������ǵ���������?�����ڣ�ֱ��д��![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1)![]() ��(2)�ٵ�
��(2)�ٵ�![]() ʱ����
ʱ����![]() ��
��![]() ��
��![]() Ϊ����������ε����Ϊ
Ϊ����������ε����Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() �ǵ���������.
�ǵ���������.
��������
��1������ͼ���������ύ����ֱ�ӵó�������������ֱ�߽�����������ֱ�߽���ʽ�������ɵó�����������
��2��������S����ACOB��S��ACP��S��POR��S��ARB��8����ʾ�������ֵı߳���������һԪ���η��������������
������һ�κ�����������Ľ���ó�����OBN����ONB��45�㣬�������ù��ɶ����Լ����������ε����ʺ�ֱ�������ε��ж����������
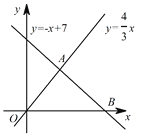
��1����һ�κ���y����x+7������������y![]() x��ͼ���ڵ�A������x�ύ�ڵ�B��
x��ͼ���ڵ�A������x�ύ�ڵ�B��
�� �������
�������![]() ��
��
��A����������3��4����
��y����x+7��0�������x��7��
��B����������7��0����
��2������P��OC���˶�ʱ��0��t��4ʱ��PO��t��PC��4��t��BR��t��OR��7��t��
�ߵ���A��P��RΪ����������ε����Ϊ8��
��S����ACOB��S��ACP��S��POR��S��ARB��8��
��![]() ��AC+BO����CO
��AC+BO����CO![]() AC��CP
AC��CP![]() PO��RO
PO��RO![]() AM��BR��8��
AM��BR��8��
�ࣨAC+BO����CO��AC��CP��PO��RO��AM��BR��16��
�ࣨ3+7����4��3����4��t����t����7��t����4t��16��
��t2��8t+12��0�������t1��2��t2��6����ȥ����
��t��4ʱ��A��P��R������Թ�������������ʱ�����6������������
��4��t��7ʱ��S��APR![]() AP��OC��2��7��t����8�������t��3��������4��t��7��
AP��OC��2��7��t����8�������t��3��������4��t��7��
������������t��2ʱ����A��P��RΪ����������ε����Ϊ8��
�����ڣ��ӳ�CA��ֱ��l����һ��D����l��AB�ཻ��Q��
��һ�κ���y����x+7��x�ύ�ڣ�7��0��������y�ύ�ڣ�0��7������
��NO��OB��
���OBN����ONB��45�㣮
��ֱ��l��y����
��RQ��RB��CD��L��
��0��t��4ʱ����ͼ1��RB��OP��QR��t��DQ��AD����4��t����AC��3��PC��4��t��
����A��P��QΪ������������ǵ�������������AP��AQ��
��AC2+PC2��AP2��AQ2����![]() AD��2��
AD��2��
��9+��4��t��2��2��4��t��2�������t1��1��t2��7����ȥ����
��AP��PQʱ 32+��4��t��2����7��t��2�������t��4 ����ȥ����
��PQ��AQʱ��2��4��t��2����7��t��2�������t1��1+3![]() ����ȥ����t2��1��3
����ȥ����t2��1��3![]() ����ȥ������t��4ʱ����������������
����ȥ������t��4ʱ����������������
��4��t��7ʱ����ͼ������ͼ������A��AD��OB��D����AD��BD��4����ֱ��l��AC��E����QE��AC��AE��RD��t��4��AP��7��t����cos��OAC![]() ������AQ
������AQ![]() ��t��4������AQ��AP����
��t��4������AQ��AP����![]() ��t��4����7��t�������t
��t��4����7��t�������t![]() ��
��
��AQ��PQʱ��AE��PE����AE![]() AP������t��4
AP������t��4![]() ��7��t���������t��5��
��7��t���������t��5��
��AP��PQʱ����P��PF��AQ��F��AF![]() AQ
AQ![]() ��t��4����
��t��4����
��Rt��APF������cos��PAF![]() ������AF
������AF![]() AP����
AP����![]() ��t��4��
��t��4��![]() ��7��t���������t
��7��t���������t![]() ��
��
������������t��1��5��![]() ��
��![]() ��ʱ��������A��P��QΪ������������ǵ�����������
��ʱ��������A��P��QΪ������������ǵ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
����x�ķ��̣�![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��![]() ��
��![]() �Ľ���
�Ľ���![]() ��
��![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��![]()
![]() ��۲��������������������ȽϹ���x�ķ���
��۲��������������������ȽϹ���x�ķ���![]() �����ǵĹ�ϵ���������Ľ���ʲô�������á����̵Ľ⡱�ĸ��������֤��
�����ǵĹ�ϵ���������Ľ���ʲô�������á����̵Ľ⡱�ĸ��������֤��
![]() �������Ĺ۲졢�Ƚϡ����롢��֤�����Եó����ۣ�
�������Ĺ۲졢�Ƚϡ����롢��֤�����Եó����ۣ�
������̵������δ֪�����䵹���ı����ĺͣ����̵��ұߵ���ʽ�������ȫ��ͬ��ֻ�ǰ����е�δ֪��������ij����������ô�����ķ��̿���ֱ�ӵý⣬����������۽����x�ķ��̣�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ����������:
��������������壬�������ˣ������ʰ�����Ҫʲô����?�����¶Թ���˵:����ֻҪ�������ϵ�һ���һ���ף��ڶ���Ŷ���������������������ĸ�Űˣ���������������������������̾��У���������ΪҪ���˶�����ʳ������ڴ�Ӧ�ˣ�
(1)������������̹���![]() �����ӣ����ڵ�
�����ӣ����ڵ�![]() ����Ӧ�� ���ף�(���ݱ�ʾ)
����Ӧ�� ���ף�(���ݱ�ʾ)
(2)��̽����(1)���е��ݵĸ�λ�����Ƕ���?(��Ҫд��̽������)
(3)��֪����������˰����¶���������?Ϊ���������⣬��������������Ľ������:
���÷�����ʾ����ѭ��С��:![]()
��:��![]() ����ʽ����ͬʱ��
����ʽ����ͬʱ��![]() ��
��
��![]() ��
��
��![]() ��:
��:![]() ��
��
��![]()
![]()
��������Ͻⷨ���������������µ���������(���ݵ���ʽ��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ����
����![]() ����
����![]() .�Ե�
.�Ե�![]() Ϊ���ģ�˳ʱ����ת����
Ϊ���ģ�˳ʱ����ת����![]() ���õ�����
���õ�����![]() ����
����![]() ��
��![]() ��
��![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() ��
��![]() .
.
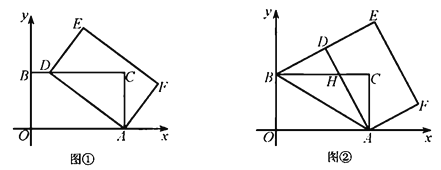
��������ͼ�٣�����![]() ����
����![]() ����ʱ�����
����ʱ�����![]() �����ꣻ
�����ꣻ
��������ͼ�ڣ�����![]() �����߶�
�����߶�![]() ��ʱ��
��ʱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
����֤![]() ��
��
�����![]() ������.
������.
��������![]() ����
Ϊ����![]() �Խ��ߵĽ��㣬
�Խ��ߵĽ��㣬![]() Ϊ
Ϊ![]() ���������
���������![]() ��ȡֵ��Χ��ֱ��д��������ɣ�.
��ȡֵ��Χ��ֱ��д��������ɣ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��OC��BO���ӳ��ߣ�OFƽ�֡�AOD����AOE=35.
��OC��BO���ӳ��ߣ�OFƽ�֡�AOD����AOE=35.
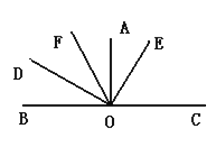
(1)���EOC�Ķ�����
(2)���BOF�Ķ�����
(3)����д��ͼ��������ȵĽ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����![]() �ļ��������������ϱ�ʾ��a�ĵ���ԭ��ľ��룬һ��أ���A��B�������Ϸֱ��ʾ��a��b����ôA��B֮��ľ���ɱ�ʾΪ|a-b|������ݾ���ֵ�ļ������岢����������������⣺
�ļ��������������ϱ�ʾ��a�ĵ���ԭ��ľ��룬һ��أ���A��B�������Ϸֱ��ʾ��a��b����ôA��B֮��ľ���ɱ�ʾΪ|a-b|������ݾ���ֵ�ļ������岢����������������⣺
��1�������ϵ���x��1����Ӧ�ĵ�ľ���Ϊ________����x��-1����Ӧ�ĵ�ľ���Ϊ________��
��2����![]() �����ֵ��
�����ֵ��
��3��ֱ��д��![]() �����ֵΪ______��
�����ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������У� ��
��![]() ��
��![]() �ζ���ʽ��
�ζ���ʽ��![]() ��
��![]() �ζ���ʽ(
�ζ���ʽ(![]() ��
��![]() ����������)����
����������)����![]() ��
��![]() һ������
һ������![]() �ζ���ʽ���ڷ�ʽ�����⣬���ʽ����ȥ��ĸ�����õ���ʽ�����⣻��
�ζ���ʽ���ڷ�ʽ�����⣬���ʽ����ȥ��ĸ�����õ���ʽ�����⣻��![]() Ϊ������)���ܷ�ʽ�ķ��Ӻͷ�ĸ������(�����)ͬһ����������ʽ��ֵ����
Ϊ������)���ܷ�ʽ�ķ��Ӻͷ�ĸ������(�����)ͬһ����������ʽ��ֵ����
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ���Խ���
���Խ���![]() ���ȷ֣���
���ȷ֣���![]() ������
������![]() .
.
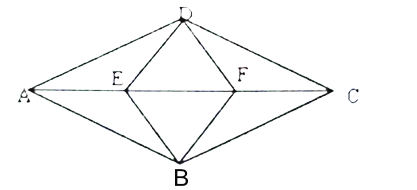
��1����֤���ı���![]() Ϊ����
����
��2��������![]() �������
�������
��3����![]() ������
������![]() �ı��ϵĵ㣬������
�ı��ϵĵ㣬������![]() �ĵ�
�ĵ�![]() �ĸ�����______��.
�ĸ�����______��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��2017��12�·ݵ��������У������������������ĸ����ڵ��������ĸ����ĺͿ�����:

A.60B.70C.80D.90
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com