
【题目】阅读下列材料,并解答问题:
阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放八....按这个方法放满整个棋盘就行.”国王以为要不了多少粮食,就随口答应了.
(1)国际象棋的棋盘共有![]() 个格子,则在第
个格子,则在第![]() 格中应放 粒米.(用幂表示)
格中应放 粒米.(用幂表示)
(2)请探究第(1)题中的幂的个位数字是多少?(简要写出探究过程)
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
“用分数表示无限循环小数:![]()
解:设![]() .等式两边同时乘
.等式两边同时乘![]() ,
,
得![]() .
.
将![]() 得:
得:![]() ,
,
则![]()
![]()
请参照以上解法求出国王输给阿基米德的米粒数.(用幂的形式表示)
【答案】(1) 263;(2) 8;(3) 264-1
【解析】
(1)观察发现,第n个格子里的米粒数是2为底数,n-1作为指数;
(2)通过计算可以看出,个位数是以4项为一组循环的,用63除以4,余数是几就与第几项的个位数相同;
(3)利用信息,这列数都乘以2,再相减即可求出.
(1)第一格放一粒米为:20,
第二格放二粒:21,
第三格放四粒:22,
第四格放八粒:23
…
按这个方法,
国际象棋共有64个格子,
则在第64格应放263粒米;
故答案为:263;
(2)∵20=1,21=2,22=4,23=8,24=16,25=32,…
![]() ,
,
∴263的末位数字与23的末位数字相同,是8;
(3)设x=1+2+22+…+263 ①.
等式两边同时乘以2,得2x=2+22+23+…+264 ②,
②-①,得x=264-1.
答:国王输给阿基米德的米粒数为264-1.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
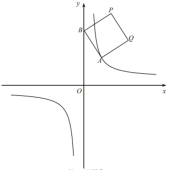
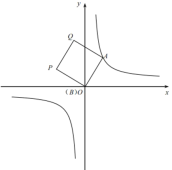
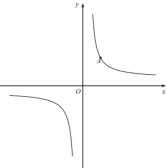
图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为正方形.在边
为正方形.在边![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() .
.
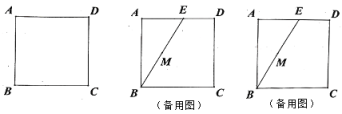
(1)利用尺规作图(保留作图痕迹):分别以点![]() 、
、![]() 为圆心,
为圆心,![]() 长为半径作弧交正方形内部于点
长为半径作弧交正方形内部于点![]() ,连接
,连接![]() 并延长交边
并延长交边![]() 于点
于点![]() ,则
,则![]() ;
;
(2)在前面的条件下,取![]() 中点
中点![]() ,过点
,过点![]() 的直线分别交边
的直线分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
①当![]() 时,求证:
时,求证:![]() ;
;
②当![]() 时,延长
时,延长![]() ,
,![]() 交于
交于![]() 点,猜想
点,猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在郴州市的日常工作中,洒水车每天都在国庆路上来回洒水.我们约定洒水车在行驶过程中,向北的行程记为正数,向南的行程记为负数.2017年8月20日这一天,某台洒水车市政工程处出发,所走的路程(单位:千米)为:+5,+7.5,-8,-3,+9.5,+2.5,-11,-3.5.问:
(1)这天收工时,这台洒水车离市政工程处多远?它在市政工程处的南边还是北边?
(2)若洒水车每走1千米耗油0.2升,请问这一天这台洒水车在洒水过程中耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
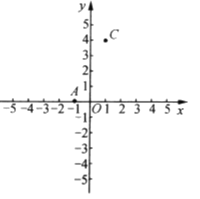
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
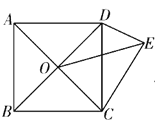
【题目】如图, ABCD 为正方形, O 为 AC 、 BD 的交点,在![]() 中,
中,![]() 90,
90, ![]() 30,若OE
30,若OE ![]() ,则正方形的面积为( )
,则正方形的面积为( )
A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
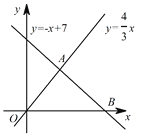
【题目】如图,已知一次函数![]() 与正比例函数
与正比例函数![]() 的图象交于点
的图象交于点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出点![]() 的坐标为 ;点
的坐标为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线l∥y轴.动点
作直线l∥y轴.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长的速度,沿
个单位长的速度,沿![]() 的路线向点
的路线向点![]() 运动;同时直线
运动;同时直线![]() 从点
从点![]() 出发,以相同速度向左平移,在平移过程中,直线
出发,以相同速度向左平移,在平移过程中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 或线段
或线段![]() 于点
于点![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 和直线
和直线![]() 都停止运动.在运动过程中,设动点
都停止运动.在运动过程中,设动点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
![]() 当
当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() ;
;
![]() 是否存在以
是否存在以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?若存在,直接写出
为顶点的三角形是等腰三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
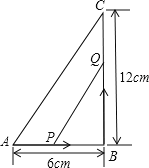
【题目】如图,在![]() 中,
中,![]() ,点P从点A开始,沿AB向点B以
,点P从点A开始,沿AB向点B以![]() 的速度移动,点Q从B点开始沿BC以
的速度移动,点Q从B点开始沿BC以![]() 的速度移动,如果P、Q分别从A、B同时出发:
的速度移动,如果P、Q分别从A、B同时出发:
![]() 几秒后四边形APQC的面积是31平方厘米;
几秒后四边形APQC的面积是31平方厘米;
![]() 若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com