解:(1)由题意,得:

,
解得:

,
∴所求抛物线的解析式为:y=-

x
2-x+4.
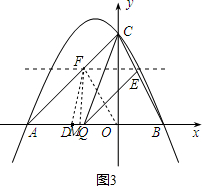
(2)设点Q的坐标为(m,0),过点E作EG⊥x轴于点G.
由-

x
2-x+4=0,
得x
1=2,x
2=-4,
∴点B的坐标为(2,0),
∴AB=6,BQ=2-m,
∵QE∥AC,
∴△BQE∽△BAC,
∴
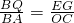
,
即
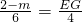
,
∴EG=

(2-m),
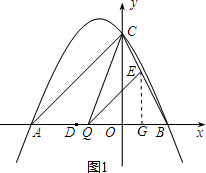
∴S
△CQE=S
△CBQ-S
△EBQ=

BQ•CO-

BQ•EG
=

(2-m)[4-

(2-m)]
=-(m+1)
2+3
又∵-4≤m≤2,
∴当m=-1时,S
△CQE有最大值3,此时Q(-1,0).
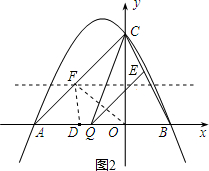
(3)存在.在△ODF中.
(ⅰ)若DO=DF,
∵A(-4,0),D(-2,0)
∴AD=OD=DF=2,
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°,
∴∠DFA=∠OAC=45°,
∴∠ADF=90°.
此时,点F的坐标为(-2,2)
(ⅱ)若FO=FD,过点F作FM⊥x轴于点M
由等腰三角形的性质得:OM=OD=1,
∴AM=3,
∴在等腰直角△AMF中,MF=AM=3,
∴F(-1,3);
(ⅲ)若OD=OF,
∵OA=OC=4,且∠AOC=90°,
∴AC=4

,
∴点O到AC的距离为2

,而OF=OD=2<2

,
∴此时不存在这样的直线l,使得△ODF是等腰三角形,
综上所述,存在这样的直线l,使得△ODF是等腰三角形,
所求点F的坐标为:F(-2,2)或(-1,3).
分析:(1)由抛物线y=ax
2+2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A(-4,0),利用待定系数法即可求得该抛物线的解析式;
(2)首先设点Q的坐标为(m,0),过点E作EG⊥x轴于点G.由(1)中的抛物线,即可求得B的坐标,即可求得AB与BQ的值,又由△BQE∽△BAC,利用相似三角形的对应边成比例,即可求得EG的值,又由S
△CQE=S
△CBQ-S
△EBQ,利用二次函数的最值的求解方法,即可求得当△CEQ的面积最大时,点Q的坐标;
(3)根据题意分别从OD=DF,DF=OF,OD=OF去分析,即可求得答案,利用等腰三角形与直角三角形的性质即可求得答案.
点评:此题考查了二次函数的综合应用,考查了待定系数求函数解析式,等腰三角形的性质,直角三角形的性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想,方程思想与分类讨论思想的应用,注意辅助线的作法.

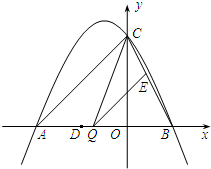 如图,抛物线y=ax2+2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A(-4,0)和B.
如图,抛物线y=ax2+2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A(-4,0)和B. ,
, ,
, x2-x+4.
x2-x+4. x2-x+4=0,
x2-x+4=0,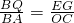 ,
,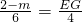 ,
, (2-m),
(2-m),
 BQ•CO-
BQ•CO- BQ•EG
BQ•EG (2-m)[4-
(2-m)[4- (2-m)]
(2-m)]

 ,
, ,而OF=OD=2<2
,而OF=OD=2<2 ,
,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).