练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

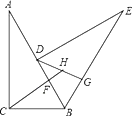
    【题目】如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．

    （1）求证：CF=DG；

    （2）求出∠FHG的度数．

    【答案】（1）SAS全等（2）120°

    【解析】试题分析：（1）在△CBF和△DBG中，根据SAS即可证得两个三角形全等，根据全等三角形的对应边相等即可证得；

    （2）根据全等三角形的对应角相等，即可证得∠DHF=∠CBF=60°，从而求解．

    试题解析：（1）证明：∵在△CBF和△DBG中，，

    ∴△CBF≌△DBG（SAS）．

    ∴CF=DG．

    （2）∵△CBF≌△DBG，∴∠BCF=∠BDG．

    又∵∠CFB=∠DFH，∴∠DHF=∠CBF=60°．

    ∴∠FHG=180°﹣∠DHF=180°﹣60°=120°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，CD⊥AB于D，求：

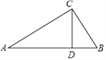
    （1）斜边AB的长；

    （2）△ABC的面积；

    （3）高CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将抛物线y＝2x向右平移4个单位，再向上平移3个单位，得到的图象的表达式为(　　)

    A. y＝2(x－4)＋3B. y＝2(x＋4)＋3C. y＝2(x－4)－3D. y＝2(x＋4)－3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

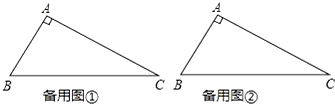
    【题目】探索研究．请解决下列问题：

    （1）已知△ABC中，∠A=90°，∠B=67.5°，请画一条直线，把这个三角形分割成两个等腰三角形．（请你选用下面给出的备用图，并把所有不同的分割方法都画出来，图不够可以自己画．只需画图，不必说明理由，但要在图中标出相等两角的度数）．

    （2）已知等腰△ABC中，AB=AC，D为BC上一点，连接AD，若△ABD和△ACD都是等腰三角形，则∠B的度数为　　（请画出示意图，并标明必要的角度）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

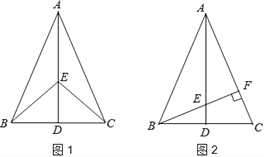
    【题目】如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．

    （1）求证：BE=CE；

    （2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

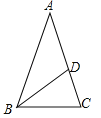
    【题目】如图，在△ABC中，AB=AC=1，BC=，在AC边上截取AD=BC，连接BD．

    （1）通过计算，判断与ACCD的大小关系；

    （2）求∠ABD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的材料：

    点A，B在数轴上分别表示有理数a，b，A，B两点之间的距离表示为|AB|.

    （1）当A，B两点中有一点在原点时，假设点A在原点，如图①所示，|AB|=|OB|=|b|=|a-b|.

    ① ②

    ③ ④

    （2）当A，B两点都不在原点时

    ①如图②所示，点A，B都在原点的右边时，|AB|=|OB|-|OA|=b-a=|a-b|；

    ②如图③所示，点A，B都在原点的左边时，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|.

    ③如图④所示，点A，B在原点的两侧时，|AB|=|OA|+|OB|=|a|+|b|=a+（-b）=|a-b|.

    解答下列问题：

    （1）数轴上表示4与2015的两点之间的距离为________，数轴上表示-与-的两点之间的距离为________，数轴上表示1.28与-8.62的两点之间的距离为__________.

    （2）有理数-6和x在数轴上的对应点分别为点A、B，如果|AB|=10，那么x为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程2x2﹣6x+k＝0有两个不相等的实数根，则实数k的取值范围是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数轴上，大于﹣2且小于4的整数的和为_____，积为_____．

    查看答案和解析>>

    同步练习册答案