Question

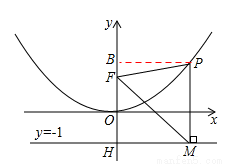
二次函数图象的顶点在原点O，经过点A（1，）；点F（0，1）在y轴上．直线y=﹣1与y轴交于点H．

（1）求二次函数的解析式；

（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP；

（3）当△FPM是等边三角形时，求P点的坐标．

 

 

Answer 1

（1）y=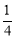x2；（2）证明见解析；（3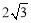）（，3）或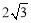（﹣，3）．

【解析】

试题分析：（1）根据题意可设函数的解析式为y=ax2，将点A代入函数解析式，求出a的值，继而可求得二次函数的解析式.

（2）过点P作PB⊥y轴于点B，利用勾股定理求出PF，表示出PM，可得PF=PM，∠PFM=∠PMF，结合平行线的性质，可得出结论.

（3）首先可得∠FMH=30°，设点P的坐标为（x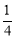，x2），根据PF=PM=FM，可得关于x的方程，求出x的值即可得出答案．

试题解析：【解析】
（1）∵二次函数图象的顶点在原点O，∴设二次函数的解析式为y=ax2.

将点A（1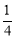，）代入y=ax2得：a=，

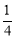∴二次函数的解析式为y=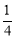x2.

（2）证明：∵点P在抛物线y=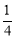x2上，

∴可设点P的坐标为（x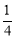，x2），

如答图。过点P作PB⊥y轴于点B，

则BF=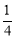x2﹣1，PB=x，

∴Rt△BPF中，.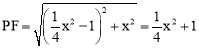

∵PM⊥直线y=﹣1，∴PM=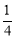x2+1.

∴PF=PM. ∴∠PFM=∠PMF.

又∵PM⊥x轴，即PM∥y轴，∴∠MFH=∠PMF. ∴∠PFM=∠MFH.

∴FM平分∠OFP.

（3）∵当△FPM是等边三角形时，∠PMF=60°，∴∠FMH=30°.

在Rt△MFH中，MF=2FH=2×2=4.

∵PF=PM=FM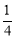，∴x2+1=4，解得：x=±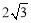.∴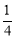x2=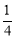×12=3.

∴满足条件的点P的坐标为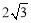（，3）或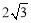（﹣，3）．

考点：1.二次函数综合题；2.待定系数法的应用；3.曲线上点的坐标与方程的关系；4.勾股定理；5.等腰三角形的性质；6.平行的性质；7. 等边三角形的性质．