
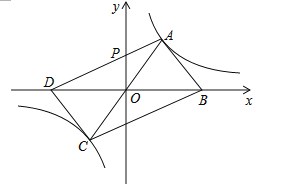
【题目】平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
【答案】(1)k=6,C(﹣2,﹣3);(2)![]() .
.
【解析】
试题分析:(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.
试题解析:(1)∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,∴3=
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,∴3=![]() ,点C与点A关于原点O对称,∴k=6,C(﹣2,﹣3),即k的值是6,C点的坐标是(﹣2,﹣3);
,点C与点A关于原点O对称,∴k=6,C(﹣2,﹣3),即k的值是6,C点的坐标是(﹣2,﹣3);
(2)∵△APO的面积为2,点A的坐标是(2,3),∴2=![]() ,得OP=2,设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,则
,得OP=2,设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,则![]() ,解得:
,解得:![]() ,即直线PC的解析式为
,即直线PC的解析式为![]() ,将y=0代入
,将y=0代入![]() ,得x═﹣4,∴OP=4,∵A(2,3),C(﹣2,﹣3),∴AC=
,得x═﹣4,∴OP=4,∵A(2,3),C(﹣2,﹣3),∴AC=![]() =
=![]() ,设点D到AC的距离为m,∵S△ACD=S△ODA+S△ODC,∴
,设点D到AC的距离为m,∵S△ACD=S△ODA+S△ODC,∴![]() ,解得,m=
,解得,m=![]() ,即点D到直线AC的距离是
,即点D到直线AC的距离是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(6,0)、 C(0,4),点B在第一象限.
(1)写出点B的坐标和长方形OABC的面积;
(2)若点D沿长方形的边从O→C→B运动,若三角形OBD的面积是长方形OABC的面积的三分之一, 求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程a(x+m)2+n=0(a,m,n均为常数,m≠0)的解是x1=-2,x2=3,则方程a(x+m-5)2+n=0的解是( )
A. x1=-2,x2=3
B. x1=-7,x2=-2
C. x1=3,x2=-2
D. x1=3,x2=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个足球与足球规定质量偏差如下:﹣3,+5,+10,﹣20(超过为正,不足为负).质量相对最合规定的是( )
A. +10 B. ﹣20 C. ﹣3 D. +5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如下表所示:
读书时间(小时) | 7 | 8 | 9 | 10 | 11 |
学生人数 | 6 | 10 | 9 | 8 | 7 |
则该班学生一周读书时间的中位数和众数分别是( )
A. 9,8 B. 9,9 C. 9.5,9 D. 9.5,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P,Q分别是双曲线![]() 在第一、三象限上的点,PA⊥
在第一、三象限上的点,PA⊥![]() 轴,QB⊥
轴,QB⊥![]() 轴,垂足分别为A,B,点C是PQ与
轴,垂足分别为A,B,点C是PQ与![]() 轴的交点.设△PAB的面积为
轴的交点.设△PAB的面积为![]() ,△QAB的面积为
,△QAB的面积为![]() ,△QAC的面积为
,△QAC的面积为![]() ,则有( )
,则有( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com