
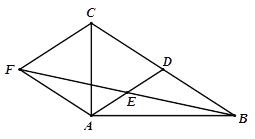
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
【答案】(1)证明见解析;(2)四边形ADCF是菱形,证明见解析.
【解析】试题分析:(1)利用AAS定理判定三角形全等即可;(2)先判定四边形的形状,再根据直角三角形斜边上的中线等于斜边的一半,得出四边形是平行四边形,再加上领边相等得出菱形即可.
试题解析:
(1)证明∵AF∥BC ∴∠EFA=∠EBD∵ E是AD的中点 ∴AE=DE ∵∠FEA=∠DEB ∴ΔAEF≌ΔDEB(4分)
(2)四边形ADCF是菱形.
理由:∵CA⊥AB∴ΔACB是RtΔ,∵AD是CD边的中线
∴AD=CD=DB.由(1)知AF=DB∴AF=CD又AF∥CD∴四边形ADCF是平行四边形
又∵DA=DC∴平行四边形ADCF是菱形.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年4月22日是第![]() 个世界地球日,今年的主题为“珍惜自然资源呵护美丽国土一讲好我们的地球故事”地球日活动周中,同学们开展了丰富多彩的学习活动,活动周期间,两位家长计划带领若干学生去参观山西地质博物馆,他们联系了两家旅行社,报价均为每人
个世界地球日,今年的主题为“珍惜自然资源呵护美丽国土一讲好我们的地球故事”地球日活动周中,同学们开展了丰富多彩的学习活动,活动周期间,两位家长计划带领若干学生去参观山西地质博物馆,他们联系了两家旅行社,报价均为每人![]() 元.经协商,甲旅行社的优惠条件是,家长免费,学生都按九折收费.乙旅行社的优惠条件是,家长、学生都按八折收费.若只考虑收费,这两位家长应该选择哪家旅行社更合算?
元.经协商,甲旅行社的优惠条件是,家长免费,学生都按九折收费.乙旅行社的优惠条件是,家长、学生都按八折收费.若只考虑收费,这两位家长应该选择哪家旅行社更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10![]() km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4![]() km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.

A.8![]() B.9
B.9![]() C.6
C.6![]() D.7
D.7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中的位置如图所示,先将
在平面直角坐标系中的位置如图所示,先将![]() 向右平移3个单位,再向下平移1个单位到
向右平移3个单位,再向下平移1个单位到![]() ,
,![]() 和
和![]() 关于
关于![]() 轴对称.
轴对称.

(1)画出![]() 和
和![]() ;
;
(2)在![]() 轴上确定一点
轴上确定一点![]() ,使
,使![]() 的值最小,试求出点
的值最小,试求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com