[题目]在平面直角坐标系中的位置如图所示.先将向右平移3个单位.再向下平移1个单位到.和关于轴对称．(1)画出和,(2)在轴上确定一点.使的值最小.试求出点的坐标．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在平面直角坐标系中的位置如图所示，先将向右平移3个单位，再向下平移1个单位到，和关于轴对称．

（1）画出和；

（2）在轴上确定一点，使的值最小，试求出点的坐标．

【答案】（1）详见解析；（2）

【解析】

（1）△ABC向右平移3个单位，再向下平移1个单位到△A1B1C1，△A1B1C1和△A2B2C2关于x轴对称，据此作图即可；

（2）依据轴对称的性质，连接BA2，交x轴于点P，此时BP+A1P的值最小，依据直线BA2的解析式，即可得到点P的坐标．

解：（1）如图所示，△A1B1C1和△A2B2C2即为所求；

（2）如图所示，连接BA2，交x轴于点P，则点P即为所求；

设直线BA2的解析式为，由B（-3，2），A2（3，-3）可得，

，解得

∴直线BA2的解析式为y=

当y=0时，

解得

∴

练习册系列答案

赢在中考全程优化单元滚动测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：

①abc＞0；②b2=4ac； ③4a+2b+c＞0；④3a+c＞0，

其中，正确的结论是______．（写出正确结论的序号）

查看答案和解析>>

科目：初中数学 来源： 题型：

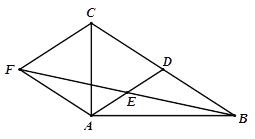
【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF＝BD；

（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】六张形状大小完全相同的小长方形卡片，分两种不同形式不重叠的放在一个底面长为m，宽为n的长方形盒子底部（如图①、图②），盒子底面未被卡片覆盖的部分用阴影表示，设图①中阴影图形的周长为，图②中两个阴影部分图形的周长和为则用含m、n的代数式=_______,=_______,若，则m=_____（用含n的代数式表示）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，直线经过点，作轴于点，将绕点逆时针旋转得到．若点的坐标为，，则点的坐标为（）

A.B.C.D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】“绿带城中挂，人在画中游”，张平和王亮同学周末相约骑行于“步移景异，心旷神怡”的温江田园绿道，他们从同一地方同时骑自行车出发(骑行过程中速度保持不变)，最后同时到达了同一个地方. 如图刻画了他们离出发点的路程(单位：米)与出发后的时间(单位：分钟)之间的关系. 已知张平中途两次休息时间相同，三段骑行时间也分别相同；王亮中途休息一次，两段骑行时间相同. 张平总的休息时间比王亮的休息时间多分钟. 请结合图中信息解答下列问题：