【题目】如图，由两个长为8，宽为4的全等矩形叠合而得到四边形ABCD，则四边形ABCD面积的最大值是( )

A.15B.16C.19D.20

参考答案：

【答案】D

【解析】

首先根据图1，证明四边形ABCD是菱形；然后判断出菱形的一条对角线为矩形的对角线时，四边形ABCD的面积最大，如图2，设AB＝BC＝x，则BE＝8x，利用勾股定理求出x的值，即可求出四边形ABCD面积的最大值是多少．

如图1，作AE⊥BC于E，AF⊥CD于F，

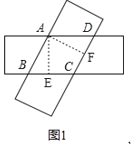
∵AD∥BC，AB∥CD，

∴四边形ABCD是平行四边形，

∵两个矩形的宽都是4，

∴AE＝AF＝4，

∵S四边形ABCD＝AEBC＝AFCD，

∴BC＝CD，

∴平行四边形ABCD是菱形．

如图2，当菱形的一条对角线为矩形的对角线时，四边形ABCD的面积最大，

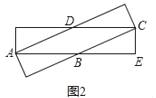
设AB＝BC＝x，则BE＝8x，

∵BC2＝BE2＋CE2，

∴x2＝（8x）2＋42，

解得x＝5，

∴四边形ABCD面积的最大值是：5×4＝20．

故选：D．

关闭