
【题目】如图,平面直角坐标系![]() 中
中![]() ,
,![]() ,
,![]() .
.

(1)作出![]() 关于直线
关于直线![]() 对称的图形△
对称的图形△![]() 并写出△
并写出△![]() 各顶点的坐标;
各顶点的坐标;
(2)将△![]() 向左平移2个单位,作出平移后的△
向左平移2个单位,作出平移后的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和△
和△![]() ,它们是否关于某直线对称?若是,请指出对称轴,并求
,它们是否关于某直线对称?若是,请指出对称轴,并求![]() 的面积.
的面积.
 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
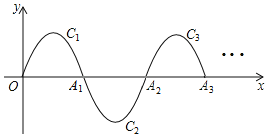
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与x轴交于点O,
,它与x轴交于点O,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;
;![]() 如此进行下去,得到一“波浪线”,若点
如此进行下去,得到一“波浪线”,若点![]() 在此“波浪线”上,则m的值为
在此“波浪线”上,则m的值为![]()
![]()
A. 4 B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一个矩形ABCD及![]() 给出如下定义:在同一平面内,如果
给出如下定义:在同一平面内,如果![]() 上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是
上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是![]() 的“随从矩形”
的“随从矩形”![]() 如图,在平面直角坐标系xOy中,直线l:
如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,
交x轴于点M,![]() 的半径为4,矩形ABCD沿直线运动
的半径为4,矩形ABCD沿直线运动![]() 在直线l上
在直线l上![]() ,
,![]() ,
,![]() 轴,当矩形ABCD是
轴,当矩形ABCD是![]() 的“随从矩形”时,点A的坐标为______.
的“随从矩形”时,点A的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(﹣3,0),B(﹣6,﹣2),C(﹣2,﹣5).将△ABC向上平移5个单位长度,再向右平移8个单位长度,得到△A1B1C1.
(1)写出点A1,B1,C1的坐标;
(2)在平面直角坐标系xOy中画出△A1B1C1;
(3)求△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.

(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com