练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

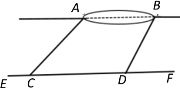
    【题目】小明想测量位于池塘两端的A、B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ ACF＝45°，再向前行走100米到点D处，测得∠ BDF＝60°．若直线AB与EF之间的距离为60米，求A、B两点的距离（结果保留根号）．

    【答案】（40+）米

    【解析】

    作AM⊥EF于点M，作BN⊥EF于点N，可以分别求得CM、DN的长，由于AB=CN-CM，从而可以求得AB的长．

    作AM⊥EF于点M，作BN⊥EF于点N，如图所示:

    由题意可得，AM=BN=60米，CD=100米，∠ACF=45°，∠BDF=60°，
    ∴CM= =60米，
    DN= 米，
    ∴AB=CD+DN-CM=100+20-60=（40+20）米，
    即A、B两点的距离是（40+20）米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

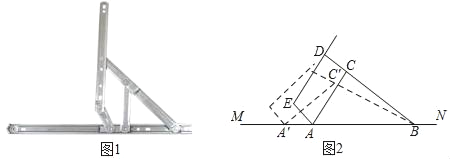
    【题目】“滑块铰链”是一种用于连接窗扇和窗框，使窗户能够开启和关闭的连杆式活动链接装置(如图1)．图2是“滑块铰链”的平面示意图，滑轨MN安装在窗框上，悬臂DE安装在窗扇上，支点B、C、D始终在一条直线上，已知托臂AC＝20厘米，托臂BD＝40厘米，支点C，D之间的距离是10厘米，张角∠CAB＝60°．

    (1)求支点D到滑轨MN的距离(精确到1厘米)；

    (2)将滑块A向左侧移动到A′，(在移动过程中，托臂长度不变，即AC＝A′C′，BC＝BC′)当张角∠C′A'B＝45°时，求滑块A向左侧移动的距离(精确到1厘米)．(备用数据：≈1.41，≈1.73，≈2.45，≈2.65)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于长为半径画弧，两弧交于一点P，连接AP并延长交BC于点E，连接EF．

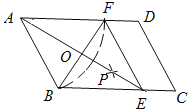
    （1）四边形ABEF是_______；（选填矩形、菱形、正方形、无法确定）（直接填写结果）

    （2）AE，BF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为________，∠ABC=________°．（直接填写结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知菱形A1B1C1D1的边长为2，∠A1B1C1=60°，对角线A1C1，B1D1相交于点O.以点O为坐标原点，分别以OA1，OB1所在直线为x轴、y轴，建立如图所示的直角坐标系．以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1，再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2，再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2，…，按此规律继续作下去，在x轴的正半轴上得到点A1，A2，A3，…，An，则点An的坐标为____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

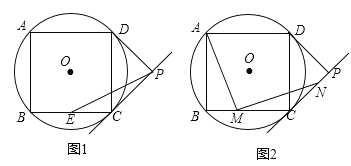
    【题目】如图，四边形ABCD是⊙O的内接正方形，AB=4，PC、PD是⊙O的两条切线，C、D为切点．

    （1）如图1，求⊙O的半径；

    （2）如图1，若点E是BC的中点，连接PE，求PE的长度；

    （3）如图2，若点M是BC边上任意一点（不含B、C），以点M为直角顶点，在BC的上方作∠AMN=90°，交直线CP于点N，求证：AM=MN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．

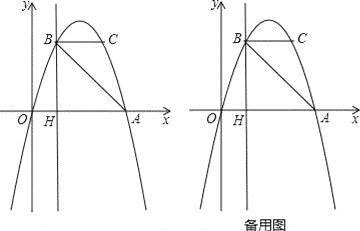
    （1）求抛物线的表达式；

    （2）直接写出点C的坐标，并求出△ABC的面积；

    （3）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；

    （4）若点M在直线BH上运动，点N在x轴上运动，当以点C、M、N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知y是x（x>0）的函数，表1中给出了几组x与y的对应值：

    表1：

    x

    …

    1

    2

    3

    …

    y

    …

    6

    3

    2

    1

    …

    ⑴以表中各对对应值为坐标，在图1的直角坐标系中描出各点，用光滑曲线顺次连接.由图像知，它是我们已经学过的哪类函数？求出函数解析式，并直接写出的值；

    ⑵如果一次函数图像与⑴中图像交于（1，3）和（3，1）两点，在第一、四象限内当x在什么范围时，一次函数的值小于⑴中函数的值？请直接写出答案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD是平行四边形，下列结论中不正确的是(　　)

    A. 当AB＝BC时，它是菱形 B. 当AC⊥BD时，它是菱形

    C. 当∠ABC＝90°时，它是矩形 D. 当AC＝BD时，它是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的γ（a，θ）变换．

    如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A1B1C1就是△ABC经γ（1，180°）变换后所得的图形．

    若△ABC经γ（1，180°）变换后得△A1B1C1，△A1B1C1经γ（2，180°）变换后得△A2B2C2，△A2B2C2经γ（3，180°）变换后得△A3B3C3，依此类推……

    △An﹣1Bn﹣1Cn﹣1经γ（n，180°）变换后得△AnBnCn，则点A1的坐标是__，点A2018的坐标是　．

    查看答案和解析>>

    同步练习册答案