
 的图象过点(1,-2),则关于
的图象过点(1,-2),则关于 的不等式
的不等式 ≤0的解集是 .
≤0的解集是 .
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象和反比例函数
的图象和反比例函数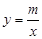 的图象的两个交点.
的图象的两个交点.
 与
与 轴的交点
轴的交点 的坐标及△
的坐标及△ 的面积;
的面积; 的解集(请直接写出答案).
的解集(请直接写出答案).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ?
?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与x轴、y轴的交点分别为A、B,以B为旋转中心,将△BOA逆时针旋转,得△BCD(其中O与C、A与D是对应的顶点).
的图象与x轴、y轴的交点分别为A、B,以B为旋转中心,将△BOA逆时针旋转,得△BCD(其中O与C、A与D是对应的顶点).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达
两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达 港.下图表示甲观光船距
港.下图表示甲观光船距 港的距离
港的距离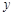 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,结合图象解答下列问题:
(小时)之间的函数关系式,结合图象解答下列问题:
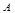 、
、 两港距离 千米,船在静水中的速度为 千米/小时;
两港距离 千米,船在静水中的速度为 千米/小时; 港的距离
港的距离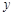 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象;
(小时)之间的函数图象;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com