

 ?
?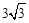
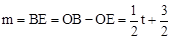 (0<t<3)
(0<t<3)
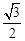 AC=
AC=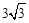 。
。
 。∴
。∴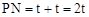 。
。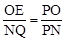 ,即
,即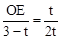 。∴
。∴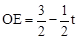 。
。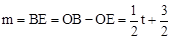 (0<t<3)。
(0<t<3)。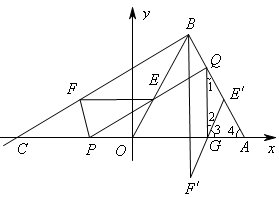
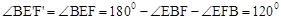 ,
,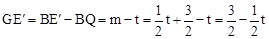 。
。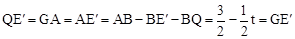 。
。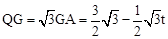 。
。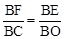 ,即
,即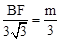 。∴
。∴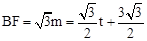 。
。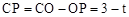 ,∴
,∴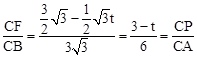 。
。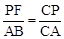 。解得
。解得 。
。 ,∴
,∴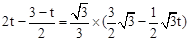 ,解得t=1。
,解得t=1。 。
。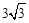 。
。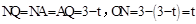 ,
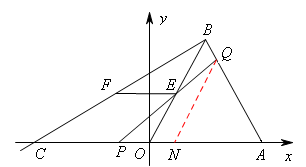
,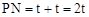 ,再由△POE∽△PNQ对应边成比例计算得
,再由△POE∽△PNQ对应边成比例计算得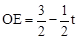 再由EF=BE易得出m与t之间的函数关系式。
再由EF=BE易得出m与t之间的函数关系式。

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 垂直的直线l5的函数表达式.
垂直的直线l5的函数表达式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
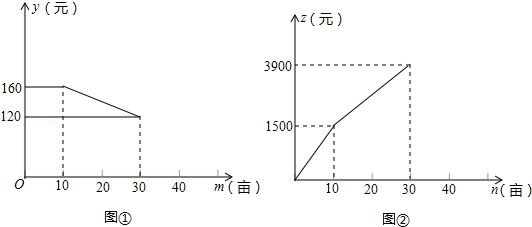
 反映了某产品的销售收入与销售量之间的关系,
反映了某产品的销售收入与销售量之间的关系, 反映了该产品的销售成本与销售量之间的关系。当销售收入大于销售成本时该产品才开始盈利。由图可知,该产品的销售量达到____________ 后,生产该产品才能盈利。
反映了该产品的销售成本与销售量之间的关系。当销售收入大于销售成本时该产品才开始盈利。由图可知,该产品的销售量达到____________ 后,生产该产品才能盈利。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 型桌椅售价150元,生产成本100元,运费2元;每套
型桌椅售价150元,生产成本100元,运费2元;每套 型桌椅售价200元,生产成本120元,运费4元,求总利润
型桌椅售价200元,生产成本120元,运费4元,求总利润 (元)与生产
(元)与生产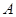 型桌椅
型桌椅 (套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润
(套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润 售价-生产成本-运费)
售价-生产成本-运费)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (千米)与时间
(千米)与时间 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.
 (千米)与时间
(千米)与时间 (小时)的函数的大致图象.
(小时)的函数的大致图象.  (千米)与时间
(千米)与时间 (小时)的函数关系式为
(小时)的函数关系式为 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com